Arquivo da categoria: Dúvidas de Física

Dúvida – Coeficiente de restituição

Deixe uma resposta

Dúvida:

Olá, sou da turma engenharia, gostaria de saber a resolução completa desta questão, eu não consegui entender bem o que seria o “coeficiente de restituição da colisão” e por consequência não conseguindo ter uma resolução. Obrigado pela atenção desde já 😀

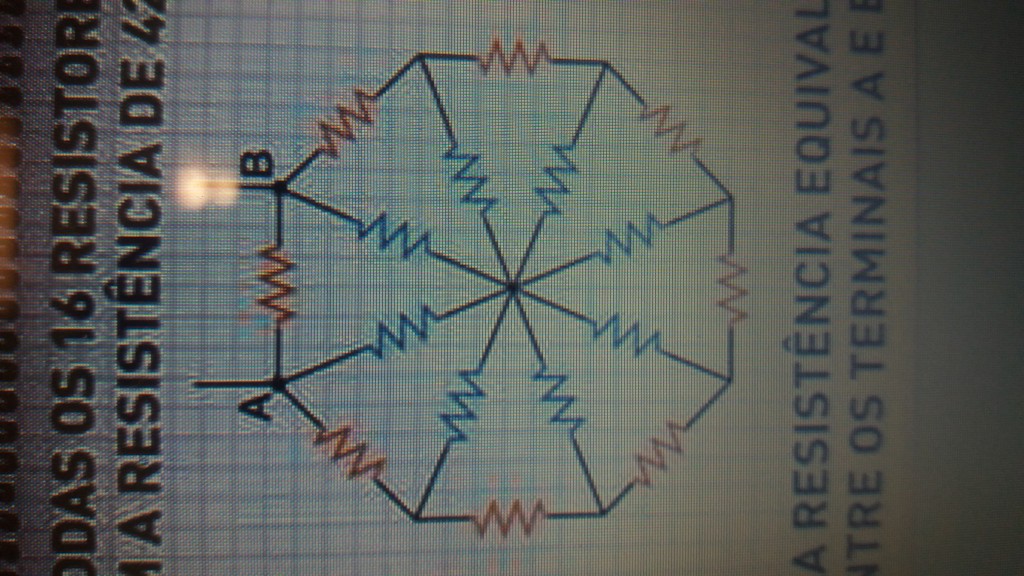
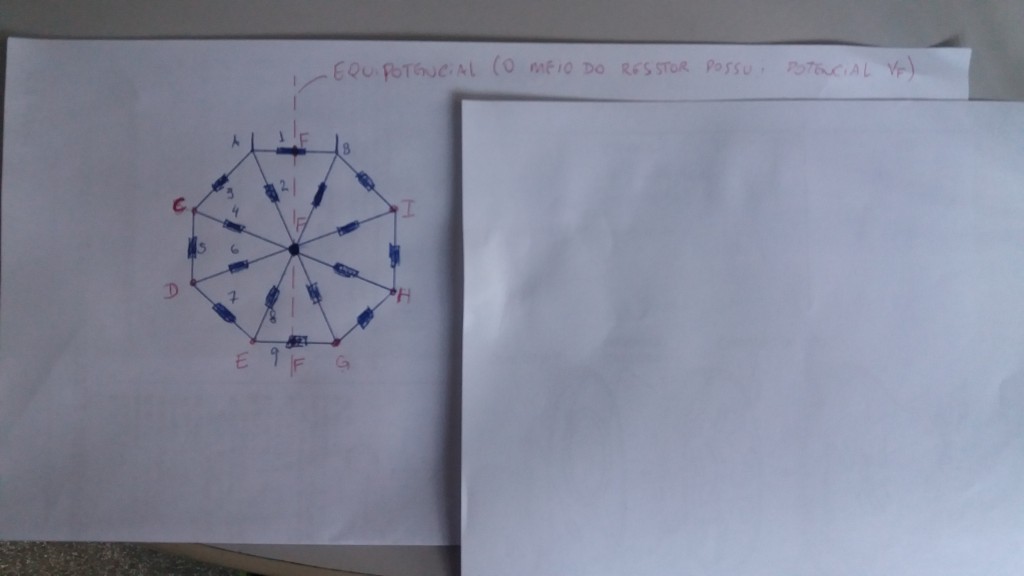
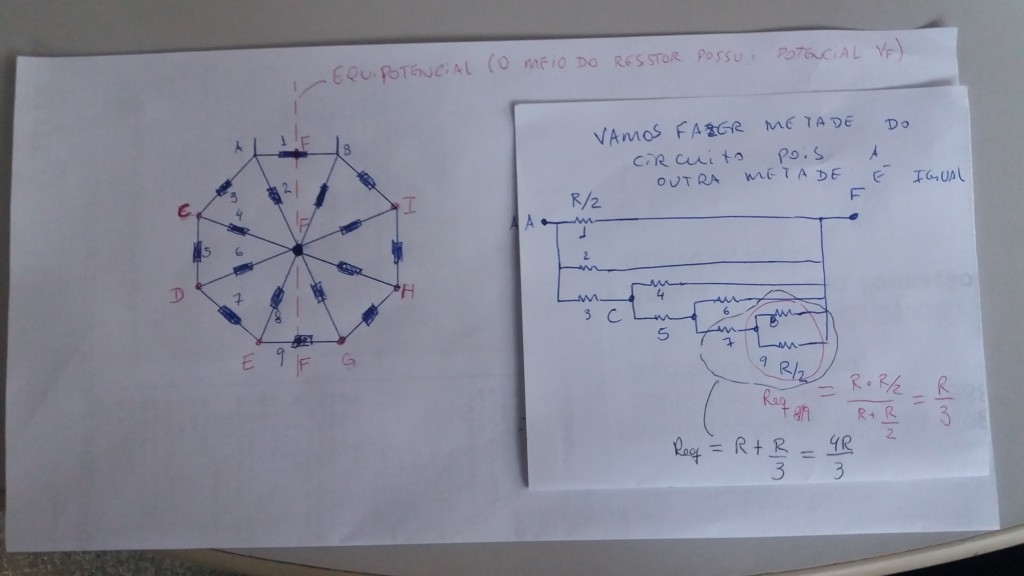
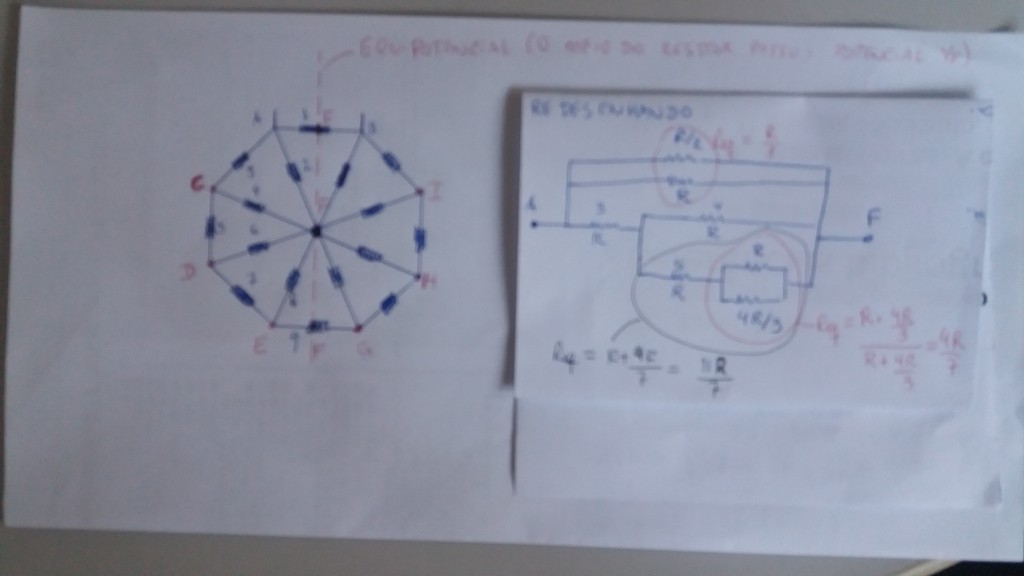
Questão: A bola A, de massa m, é liberada a partir do repouso de um edifício exatamente quando a bola B, de massa 3m, é lançada verticalmente para cima a partir do solo. As duas bolas colidem quando a bola A tem o dobro da velocidade de B e sentido oposto. O coeficiente de restituição da colisão é dado por e = 0,5. Determine a razão das velocidades, |Va/Vb|, logo após o choque.

Coeficiente de restituição

Primeiramente, vamos à sua definição:

$$e=\frac{v’_A-v’_B}{v_B-v_A} $$

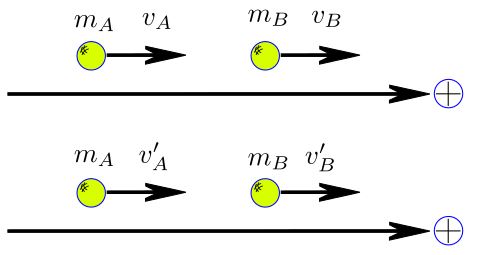
Dois referenciais positivos para a direita representando duas esferas, de massas heme a e heme b. Inicialmente, as esferas possuem velocidades vê a e vê b, porém após as colisões, adquirem velocidades vê linha a e vê linha b.
Referencial que usamos para definir o coeficiente de restiruição

Vamos fazer o estudo da colisão em uma dimensão. No caso bidimensional, decompomos as velocidades num eixo que coincida com a direção das forças envolvidas. Vamos, no entanto, estudar no caso unidimensional.

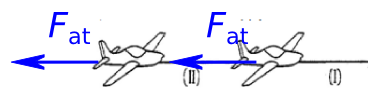
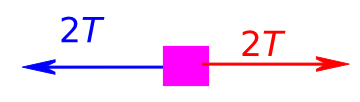
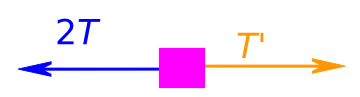
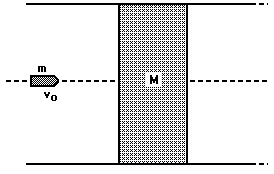
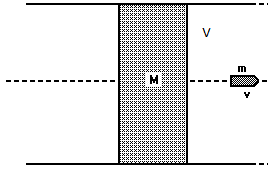
Observe a figura acima: nela temos um referencial, positivo para a direita, dois objetos que sofrerão uma colisão; as velocidades antes da colisão, dos corpos A e B, são respectivamente \( v_A\) e \(v_B\) e após a colisão \(v’_A\) e \(v’_B\), respectivamente; as massas são \(m_A\) e \(m_B\).

Voltemos agora à definição de coeficiente de restituição: $$e=\frac{v’_A-v’_B}{v_B-v_A} .$$ Em módulo, isso corresponde à razão entre a velocidade relativa após a colisão e a velocidade relativa antes da colisão. Tal coeficiente nos permite determinar a energia dissipada em uma colisão, porém é mais frequente trabalharmos com a conservação da quantidade de movimento quando trabalhamos com o coeficiente de restituição.

Veja isso numa outra postagem neste site (aprofundamento): http://estudeadistancia.professordanilo.com/?p=290

Quando trabalhamos com o coeficiente de restituição \(e\) podemos classificar a colisão em:

  • \(e=0\): colisão totalmente inelástica (ambos os corpos, após a colisão, permanece grudado, afinal, a velocidade relativa após a colisão é nula \( v’_A-v’_B =0 \) e a perda de energia cinética é a máxima possível).
  • \(0\leq e \leq 1\): colisão parcialmente elástica (ou inelástica), perdendo parte da energia cinética.
  • \(e=1\): colisão totalmente elástica, conservando totalmente a energia cinética.

Numa explosão, a energia cinética do sistema aumenta, por isso alguns autores consideram que uma colisão com explosão corresponde à uma colisão super elástica (\(e>1\)).

Sem mais detalhes, vamos para a resolução.

Questão ITA 2022: A bola A, de massa m, é liberada a partir do repouso de um edifício exatamente quando a bola B, de massa 3m, é lançada verticalmente para cima a partir do solo. As duas bolas colidem quando a bola A tem o dobro da velocidade de B e sentido oposto. O coeficiente de restituição da colisão é dado por e = 0,5. Determine a razão das velocidades, |Va/Vb|, logo após o choque.

Vamos considerar um referencial positivo para baixo (no sentido do campo gravitacional).

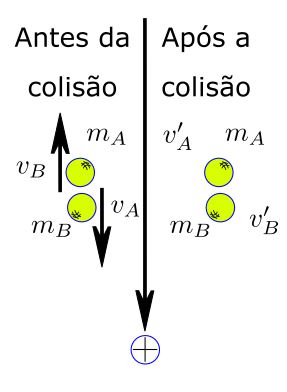
Referencial adotado para as duas esferas como positivos para baixo. Antes da colisão, a bola a possui velocidade positiva e a esfera b com velocidade negativa, isto é, a possui velocidade para baixo e b para cima. Após a colisão, as velocidades das esferas a e b são inicialmente desconhecidas. Para resolver o problema, devemos lançar mão da conservação da quantidade de movimento e do coeficiente de restituição.
Referencial adotado

Vamos começar pela conservação da quantidade de movimento (\(\vec Q = m\cdot \vec V\)). Ou seja, a quantidade de movimento antes da colisão é igual à quantidade de movimento após a colisão: \[\vec Q _{antes\; da\; colisão}=\vec Q_{após\; a\; colisão}\Rightarrow\] \[Q_A+Q_B=Q’_A+Q’_B\Rightarrow\] \[m_A\cdot v_A+m_B\cdot v_B=m_A\cdot v’_A+m_B\cdot v’_B.\]

Substituindo os dados do enunciado, que passaremos para o referencial escolhido:

  • \(m_A=m\);
  • \(v_A=-2v_B=2v\);
  • \(m_B=3m\);
  • \(v_B=-v\).

Ou seja:
\[m\cdot 2v+3m\cdot (-v)=m\cdot v’_A+3m\cdot v’_B\Rightarrow\] \[2v-3v=v’_A+3 v’_B\Rightarrow\] \[v’_A=-v-3 v’_B. \;\;\;\;\;\rm{(Equação \;01)}\]

Vamos agora utilizar a equação do coeficiente de restituição elástica: \[
e=\frac{v’_A-v’_B}{v_B-v_A} \Rightarrow\] \[
0,5=\frac{v’_A-v’_B}{-v-2v} \Rightarrow\] \[v’_A-v’_B=-1,5v. \;\;\;\;\; \rm{(Equação \; 02)}\]

Substituindo a equação 01 na equação 02, obtemos a velocidade de B depois da colisão: \[v’_A-v’_B=-1,5v \Rightarrow\] \[ -v-3 v’_B -v’_B=-1,5v \Rightarrow\] \[ -4 v’_B =-0,5v \Rightarrow\] \[ v’_B =\frac{v}{8} . \;\;\;\;\; \rm{(Equação \; 03)} \]

Substituindo o resultado da equação 03 na equação 01: \[v’_A=-v-3 v’_B \Rightarrow\] \[v’_A=-v-3 \frac v 8 \Rightarrow\] \[v’_A=-\frac {8v}{8}- \frac{ 3v}{ 8} \Rightarrow\] \[v’_A=-\frac{11v}{8}. \;\;\;\;\;\rm{(Equação \; 04)}\]

Finalmente voltemos ao enunciado: queremos |Va/Vb| que, nas variáveis adotadas na resolução, corresponde à \(\left|\frac{v’_A}{v’_B}\right|\). Calculando, então, a razão entre o resultado apresentado na equação 04 e o resultado da equação 03, temos: \[\left|\frac{v’_A}{v’_B}\right|=\left|\frac{\frac{-11v}{8}}{\frac{v}{8}}\right|=\left|\frac{-11v}{8}\cdot\frac{8}{v}\right|=|-11|=11.\]

Portanto, a resposta é 11. 😉

Espero que tenha entendido. Caso contrário, volte a escrever no formulário, disponível na página do professor, ou envie-me um e-mail ou, ainda, se preferir, comente por aqui mesmo, nesta postagem. Não se preocupe: pode inventar um e-mail falso sem precisar se identificar.

Resposta à pergunta da Rebeca

2 respostas

Resposta à pergunta feita no dia 8 de maio de 2017 por Rebeca:

Olá professor. Você poderia me ajudar a resolver este problema de física lançado em uma página do Facebook? Não sei como achar a resistência equivalente nesse caso. Não cosegui anexar a imagem, então segue o link: https://m.facebook.com/FisicaTotal/photos/a.510264229015086.109074.500833719958137/1504681772906655/?type=3&source=48
Muito obrigada!

Rebeca, irei responder mais uma vez…
Segue a imagem da pergunta:

problema

Primeiro vamos dar nome aos pontos:

RESP.parte1

Depois representamos metade do circuito fazendo um curto circuito na linha vertical pontilhada, uma vez que temos uma simetria no problema. RESP.parte2

Agora saímos calculando algumas resistências equivalentes: RESP.parte3

Por fim chegamos na resposta:

 

RESP.parte4

Exemplo semelhante:

http://osfundamentosdafisica.blogspot.com.br/2010/10/resolucao-do-desafio-de-mestre-especial_23.html

Link da dúvida:

http://estudeadistancia.professordanilo.com/?page_id=119#comment-271

 


Dúvida Respondida

Deixe uma resposta

Respondendo dúvida referente à questão abaixo:

(Ufrs) Analise as afirmativas, a seguir, identificando a INCORRETA. 

a) Quando um condutor eletrizado é colocado nas proximidades de um condutor com carga total nula, existirá força de atração eletrostática entre eles.
b) Um bastão eletrizado negativamente é colocado nas imediações de uma esfera condutora que está aterrada. A esfera então se eletriza, sendo sua carga total positiva.
c) Se dois corpos, inicialmente neutros, são eletrizados atritando-se um no outro, eles adquirirão cargas totais de mesma quantidade, mas de sinais opostos.
d) O pára-raio é um dispositivo de proteção para os prédios, pois impede descargas elétricas entre o prédio e as nuvens.
e) Dois corpos condutores, de formas diferentes, são eletrizados com cargas de -2$\mu$C e +1$\mu$C. Depois que esses corpos são colocados em contato e afastados, a carga em um deles pode ser -0,3$\mu$C

A dúvida é: porque o gabarito é a letra D e não E.

Indo diretamente ao ponto: os pára raios são dispositivos de proteção, porém eles não impedem a descarga atmosférica: pelo contrário, ele facilita a descarga sobre si. Ou seja, ele “atrai” o raio para que caia nele e não em outros pontos produzindo danos materiais ou imateriais (acidentes envolvendo pessoas ou animais ou mesmo plantas, como árvores). Você pode entender melhor o fenômeno buscando por “poder das pontas”

A alternativa E está imprecisa: ao dizer que dois corpos estão eletrizados com cargas Q1 e Q2 somos quase que automaticamente levados a dizer que a carga de cada um, depois de terem entrado em contato elétrico e se afastados, será a média das cargas:
$$Q_{final}=\frac{Q_1+Q_2}{2}=-0,33 \rm{\mu C}$$
que é aproximadamente o que se apresenta na alternativa. Contudo, isso só é válido se os corpos forem idênticos, caso sejam diferentes essa fórmula não vale e só é possível afirmar a carga de cada um conhecendo-se a capacitância de cada. Como isso não foi dado não podemos afirmar qual deve ser a carga de cada corpo, portanto a alternativa E está incorreta.

As demais alternativas estão corretas!

 


Aceleração da gravidade próxima à superfície da Terra

Deixe uma resposta

Em geral, temos duas fórmulas para calcular a força gravitacional:

$$P=mg$$

e

$$F=\frac{GMm}{d^2}$$

Mas quais as diferenças e semelhanças entre elas? Na verdade, ambas são totalmente equivalentes, pois se considerarmos uma região próxima à da Terra, podemos assumir que a gravidade é constante, assim, igualando as duas forças (pois são uma única força), temos:

$$mg=\frac{GMm}{d^2}\Rightarrow g=\frac{GM}{d^2}$$

Se $d$ for o raio da Terra, temos o valor da gravidade na superfície do planeta.

Mas para deixar esta ligação entre o que vemos quando estudamos fenômenos na superfície da Terra e a Gravitação Universal, vamos tomar o seguinte exemplo: usando as equações da gravitação universal determine a equação da variação da energia potencial de um corpo na superfície da Terra ao ser levado de um ponto à outro sendo este último à uma altura $h$ acima do primeiro. Assuma que esta altura é muito menor que o raio da Terra.

Lembrando que a energia potencial gravitacional na gravitação universal é dada por:

$$U=-\frac{GMm}{d}$$

a variação, ao ir do ponto mais baixo para o mais alto, será:

$$\Delta U=-\frac{GMm}{R+h}-\left(-\frac{GMm}{R}\right)=GMm\left(\frac{1}{R}-\frac{1}{R+h}\right)\Rightarrow$$

$$\Delta U=GMm\left(\frac{R+h-R}{R(R+h)}\right)=GMm\left(\frac{h}{R(R+h)}\right)$$

Temos agora um resultado interessante, pois $R+h\approx R$ pois $h<<R$. Além disso vimos que

$$g=\frac{GM}{R^2}$$

na superfície da Terra. Portanto:

$$\Delta U\approx GMm\left(\frac{h}{R^2)}\right)$$

Ou seja:

$$\Delta U\approx mgh$$

 

 


Resolução questão 8 AFA – Física 2002

5 respostas

Mais uma dúvida respondida:

Teria como resolver está questão?
(AFA 2002) Um avião reboca dois planadores idênticos de massa \(m\), com velocidade constante. A Tensão no cabo(II) é \(T\). De repente o avião desenvolve uma aceleração a. Considerando a força de resistência do ar invariável , a tensão no cabo (I) passa a ser
a) \(T+m\cdot a\)
b) \(T+2m\cdot a\)
c) \(2T+2m\cdot a\)
d) \(2T+m\cdot a\)
Obs: desculpe mas não consegui o desenho.

Olá, achei a questão.
http://www.futuromilitar.com.br/portal/attachments/article/17/2002-AFA-Fisica.pdf
É a número 8.


Vamos lá.

Primeiro vamos à figura:

Se os planadores são idênticos e se movem com velo
cidade constante, então a força de resistência do ar é igual em ambos e vale também \(T\) (note que o avião II é o de trás e está sujeito às forças peso e de sustentação, que não nos interessa no problema, e a tração e o atrito com o ar, que devem ser iguais para que a resultante seja nula).

Como o fio I transpor ambos os aviões, a tração neste fio deve ser de \(2T\) (para anular o efeito do atrito de ambos os planadores).

Se o avião adquire aceleração a, então o fio I deverá fornecer uma força adicional \(F=2m\cdot a\) sendo \(m\) a massa de cada planador. Isso porque a força de atrito é invariável, logo o fio deve manter a força inicial e acrescentar \(F\), pois o fio I quem “puxa” ambos os planadores.

Espero que tenha entendido: note que o fio I é o responsável por acelerar ambos os planadores.

Resposta: C

 

Adendo:

Na situação inicial, a tensão no cabo II é \(T\), conforme desenho a seguir.

afa001

Se pensarmos apenas no planador de trás, a resultante sobre ele é zero (aceleração nula), assim, sobre ele existe uma força de atrito conforme desenho abaixo (só do planador de trás).

afa002

Com isso podemos ver que, se a resultante no avião de trás for zero, então a força de atrito do ar só pode ser igual à de tração: $$F_{at}=T$$

Se os dois planadores são idênticos, então a força de resistência do ar em ambos também são idênticos.

afa003

Vamos agora pensar nos dois aviões como sendo um corpo só, pois o fio I quem puxa ambos, então podemos fazer isso sem prejuízo algum. Vou representar por um retângulo apenas.

afa004

Observe que estamos representando os dois aviões como sendo apenas um corpo. Agora, ainda na situação inicial, podemos afirmar que a resultante é nula. Ou seja, a tração no fio I deve anular as forças de atrito em ambos os planadores. Vamos de novo ao esquema:

afa005

Como se \(T=F_{at}\Rightarrow 2T=2F_{at}\), podemos redesenhar da seguinte forma:

afa006

Isso porque não foi dada nenhuma informação sobre a força de atrito, só que a tração valia \(T\).

Agora surge uma nova situação em que o sistema é acelerado. Assim, surge uma tração no fio I

fig007

Voltando para a representação dos dois planadores como sendo o quadrado dos esquemas anteriores, temos:

afa007

Agora sim, vamos usar a segunda lei de Newton. Você deve se lembrar que a resultantes das forças (no caso, a diferença dos módulos \(F_{res}=T’-2T\)) deve ser igual à massa do sistema acelerado vezes a aceleração \(a\): $$F_{res}=m\cdot a$$

A massa total no entanto é \(2m\), assim usando a segunda lei de Newton: $$F_{res}=2m\cdot a\Rightarrow T’-2T=2m\cdot a\Rightarrow$$

$$T’=2T+2m\cdot a$$

 

 

 


Dúvida: questão AFA – 2014

9 respostas

O seguinte comentário foi postado em Pergunte ao Professor Danilo por Dirlei santos:

58 – Um estudante montou um experimento com uma rede de difração de 1000 linhas por milímetro, um laser que emite um feixe cilíndrico de luz monocromática de comprimento de onda igual a m 4.10−7 e um anteparo, conforme figura abaixo.

afa2015-58
O espectro de difração, observado no anteparo pelo estudante, foi registrado por uma câmera digital e os picos de intensidade apareceram como pequenos pontos
brilhantes na imagem.
Nessas condições, a opção que melhor representa a imagem do espectro de difração obtida pelo estudante é:

a) . . .
b) . . . .
c) . . . . .
d) . . . . . . .

Não entendi essa questão, teria como me explicar ? Fica a vontade que eu gosto de física, vou tentar entender ao máximo.

Demorei um pouco para responder porque não queria colocar a resolução apenas com a fórmula: pensei em explicar o que está acontecendo.

Primeiramente, vamos ao que é rede de difração: imagine uma placa com vários cortes ao longo delas, todos paralelos entre si. Os cortes têm largura pouco maior que o comprimento de onda da onda incidente. Um exemplo disso é o cd (ou dvd e o blu-ray). Veja a foto abaixo com um experimento feito em casa com laser verde e um cd sem a parte prateada.

Pedaço de CD

Acima, um pedaço de CD sem a parte metálica. Abaixo o pedaço de CD fixo em um prendedor de papel.CD em um suporte

Ao passar o laser por ele, o que acontece?

Figura de difração da redeOs pontos que você vê é a imagem de difração da rede que existe no cd. Usei o laser verde de comprimento de onda de 532 nm, assim, além de resolver o exercício vamos calcular a distância entre duas linhas no cd. Abaixo, a distância da rede (cd) ao anteparo (parede).

Distância da Rede ao Anteparo

Vamos ao exercício.

Se procurar a solução na internet vai ver que se usam a fórmula

$$d \; \rm{sen} \theta = m \lambda $$

Vamos demonstrar esta fórmula.

Primeiro, você deve saber um pouco sobre interferência de ondas. Lembra-se que duas ondas emitidas por duas fontes em fase (em fase quer dizer que quando uma onda produzida está “subindo”, a outra também está, e quando está “descendo”, a outra também está) quando as duas se encontram pode haver interferência construtiva e destrutiva?

Se a diferença entre as distâncias percorridas por ambas as ondas for um múltiplo inteiro do comprimento de onda \(\lambda\) então ocorrerá uma interferência construtiva. É importante você saber do que estou falando para entender o restante! Se não souber, pode perguntar.

Vamos lá: abaixo está representado o perfil da rede de difração que estamos estudando:

refeDifracao

À esquerda está representado o laser e à direita os pontos de máximos (onde ocorre interferência construtiva). Cada fenda na rede se comporta como se fosse uma fonte emitindo uma onda em fase. Vamos dar um “zoom” na rede e analisar um raio de luz que sai de cada fenda:

interferencia rede

Na figura estão representados os raios que saem da rede e atingem o ponto onde ocorre o primeiro máximo de interferência, isto é, o primeiro ponto brilhante contado do centro para fora, mas desconsiderando o máximo central.

Como a distância entre as fendas d é muito pequena comparada com a distância entre a rede e o anteparo podemos considerar os raios que saem das fendas como paralelos. Na figura à direita está representado um trecho da rede onde está sendo mostrado a distância d entre duas fendas e a diferença de caminho entre dois raios consecutivos, que é dada por \(d\;\rm{sen} \theta\). Assim, temos a fórmula, pois a diferença de caminho deve ser um múltiplo inteiro (que chamaremos de \(m\)) de \(\lambda\):

diferença de caminho = número inteiro vezes comprimento de onda \(\Rightarrow\)

$$d \; \rm{sen} \theta = m \; \lambda.$$

Note que o enunciado nos deu a quantidade de linhas por milímetro, assim sabemos que a distância entre cada fenda é:

$$d=\frac{1\; \rm{mm}}{1000}=1\cdot 10^{-6}\;\rm m.$$

A pergunta é quantos máximos o estudante enxerga no anteparo. Para que apareça um ponto brilhante na parede, é necessário que \(\theta < 90^o\), pois se \(\theta > 90^o\) a luz foi refletida. Assim, para a condição de \(\theta = 90^o\) temos:

$$d \; \rm{sen} \theta = m \; \lambda \Rightarrow$$

$$1\cdot 10^{-6}\;\rm{sen}90^o=m\cdot 4\cdot 10^{-7}\Rightarrow$$

$$m=\frac{10}{4}\Rightarrow$$

$$m=2,5.$$

Como \(m\) deve ser inteiro, devemos arredonda-lo para menos, pois \(m = 3\) implica em \(\theta > 90^o\). Assim, temos que \(m = 2\).

Ou seja, estamos falando do segundo máximo, sem contar o central. Como a imagem é simétrica, temos mais dois pontos do outro lado, isto é, temos 5 pontos de máximos.

$$\rm{Resposta\;C}.$$

Voltando ao nosso exemplo, que montei com um CD,  você deve ter reparado que apareceram apenas três pontos. Mesmo aproximando o CD da parede o número não aumenta.

Vamos tentar calcular o número de linhas por unidade de comprimento do CD?

rede difracao

Por trigonometria, pelo desenho anterior, vemos que

$$\rm{tg}=\frac{y}{D}$$

Como em nosso experimento \(m = 1\), \(y=7\;\rm{cm}\) e \(D=17\;\rm{cm}\), podemos montar o seguinte sistema:

$$\left\{\begin{matrix}
d\;\rm{sen}\theta=m\;\lambda\\
\rm{tg}\theta=\frac{y}{D}
\end{matrix}\right.
\Rightarrow
\left\{\begin{matrix}
d\;\rm{sen}\theta=1\cdot532\cdot10^{-9}\\
\rm{tg}\theta=\frac{7}{17}
\end{matrix}\right.
\Rightarrow $$

$$\left\{\begin{matrix}
d\;\rm{sen}\theta=532\cdot10^{-9}\\
\theta=22,38^o
\end{matrix}\right.$$

O ângulo eu descobri usando uma calculadora científica. Assim, substituindo o resultado da equação de baixo na equação de cima e usando uma calculadora científica, temos:

$$d\;\rm{sen}22,38^o=532\cdot10^{-9}\Rightarrow d\cdot0,381=532\cdot10^{-9}\Rightarrow $$
$$d=1,397\cdot10^{-6}\;\rm m$$

Ou seja, quase 1,4 \(mu\;\text{m}\) entre uma ranhura e outra.

O número de ranhuras por milímetro é \(\frac{1}{d}\) sendo d em milímetro, ou seja:

$$\frac{1}{1,4\cdot 10^{-3} \;\rm{mm}}=714 \; \rm{ranhuras}\;\rm{por}\;\rm{mm}$$

Segundo a literatura, o valor é de 625 ranhuras por mm. Não está tão longe assim para um experimento tão simples, feito com régua, em casa.

Vamos voltar ao desenho anterior.

rede difracao

Muitas vezes a seguinte aproximação pode ser feita:

$$\rm{sen}\theta\approx\rm{tg}=\frac{y}{D}$$

Se assim for, podemos reescrever o sistema anterior tornando-o mais simples:

$$\left\{\begin{matrix}
d\;\rm{sen}\theta=m\;\lambda\\
\rm{sen}\theta\approx\frac{y}{D}
\end{matrix}\right.
\Rightarrow$$
$$d=\frac{m\;\lambda\;D}{y}$$


UESB 2015 – Cad 3

Deixe uma resposta

Resposta à dúvida postada por felipe em :

Sobre a dúvida: “eu sempre confundo funcao de estado com calor e trabalho . me explique de uma forma mais facil por favor .”, vamos lá.

Função de estado, de forma mais ou menos simplificada, são as variáveis que depende do estado (situação atual do gás, por exemplo). Digamos que você tenha duas amostras de gás à mesma temperatura, com o mesmo volume e mesma pressão. Concorda que a pressão, temperatura e volume são variáveis (grandezas físicas) que não dependem de como você as obteve? Isso seria uma variável de estado!

Melhorando o exemplo: digamos que você aqueça o gás e o expanda, depois o comprima e o faça esfriar até a temperatura inicial. A pressão voltará a situação inicial! Logo estas três grandezas são variáveis de estado. Além delas, uma grandeza um pouco abstrata, a entropia, também é variável de estado.

Calor seria uma energia térmica que você injeta no sistema, por exemplo, acendendo uma chama próxima à um reservatório com o gás em estudo. Fornecendo calor ao gás, você fornece energia à ele.

Há outra forma de fornecer ou retirar energia do sistema sem dar calor. Esta forma é através do trabalho. Por exemplo: se você pegar uma seringa vazia, puxar o êmbolo para enche-la de ar, tapar a saída e empurrar o êmbolo com força o gás sofrerá um pequeno aquecimento. Mas olha que interessante: você aqueceu o gás sem dar calor! Você realizou trabalho sobre o gás, dando-le energia (aquecendo-o).

Espero ter ajudado na sua dúvida.

Sobre a questão 14, da provas disponível em http://www.comportall.com.br/provas/UESB2015_cad3.pdf e transcrita abaixo:

Escutam-se com frequência pedidos para que se conserve energia. De acordo com a 1$^a$ lei da Termodinâmica, a energia sempre se conserva, embora algumas formas de energia sejam mais úteis do que outras.

Com base nos conhecimentos da Termodinâmica, analise as afirmativas e marque com V as verdadeiras e com F, as falsas.

( ) O rendimento de uma máquina térmica é a razão entre trabalho efetuado pela máquina e o calor recebido do reservatório quente.

( ) É possível remover energia térmica de um único reservatório e convertê-la completamente em trabalho, sem que ocorram outras mudanças.

( ) A máquina de Carnot é uma máquina reversível, que opera entre dois reservatórios, efetuando ciclos de Carnot.

( ) A entropia, tal como a pressão, o volume, a temperatura e o calor, é uma função do estado de um sistema.

A alternativa que contém a sequência correta, de cima para baixo, é a

01) F F V V

02) F V F V

03) V V F F

04) V F V F

05) V F F V

Resolução:

Primeira afirmativa: “O rendimento de uma máquina térmica é a razão entre trabalho efetuado pela máquina e o calor recebido do reservatório quente.” Isto está correto, pois o rendimento se refere à eficiência da máquina, isto é, a razão entre o que se deseja obter (trabalho) e o custo pago (calor retirado da fonte quente): $$\eta=\frac{\tau}{Q_{quente}}$$

Segunda afirmativa: “É possível remover energia térmica de um único reservatório e convertê-la completamente em trabalho, sem que ocorram outras mudanças.” Falso: considero a frase um pouco imprecisa, pois na verdade seria impossível remover energia térmica e convertê-la completamente em trabalho se estivermos pensando em um ciclo termodinâmico, isto é, a cada certo intervalo de tempo o sistema retorna ao seu estado original. A afirmativa seria verdadeira se pensarmos em um processo: por exemplo, num processo isotérmico (não num ciclo) todo o calor pode ser transformado em trabalho (pela primeira lei da termodinâmica: $Q=\Delta U + \tau$). Porém o que esta questão provavelmente queria avaliar é o conhecimento do candidato sobre a impossibilidade de criar uma máquina térmica com rendimento de 100%.

Terceira afirmativa: “A máquina de Carnot é uma máquina reversível, que opera entre dois reservatórios, efetuando ciclos de Carnot.” Correto: o ciclo de Carnot é um ciclo que não altera a entropia total do universo. Sistemas cuja entropia não varia são sempre reversíveis e isto tem a ver com o fato de que é o ciclo de Carnot que possui a maior eficiência possível.

Quarta afirmativa: “A entropia, tal como a pressão, o volume, a temperatura e o calor, é uma função do estado de um sistema.” Falso: a entropia, a pressão, a temperatura e o volume são variáveis de estado, já o calor não.

RESPOSTA: 04


UNESP – IMPULSO E QUANTIDADE DE MOVIMENTO

Deixe uma resposta

Um bloco de madeira de massa M pode deslizar livremente e sem atrito dentro de um tubo cilíndrico. Uma bala de massa m, movimentando-se com velocidade v0 ao longo do eixo horizontal do cilindro, como mostra a figura a seguir, perde 36% de sua energia cinética ao atravessar o bloco.

 projetil_antes_do_bloco
Após ter sido atravessado pela bala, o bloco, que estava inicialmente em repouso, passa a movimentar com velocidade V. Mostre que $V=\frac{mv_0}{5M}$.

(Despreze efeitos da força da gravidade sobre a trajetória da bala).

RESOLUÇÃO

Antes da colisão, a quantidade de movimento do sistema era de $mv_0$ da esquerda para a direita. Esta quantidade deve se conservar após a colisão. Assim:

$$mv_0=MV+mv$$

Em que V é a velocidade do bloco após o impacto e v a velocidade da bala após atravessar o bloco, conforme a figura a seguir.

projetil_depois-do-bloco

Segundo o enunciado, a bala perde 36% de sua energia cinética, assim, sendo $E_0$  a energia cinética da bala antes de atravessar o bloco e $E_f$ a energia cinética após atravessá-lo, temos:

$$E_f=0,64E_0$$

Substituindo os dados (literais), encontramos:

$$\frac{mv_0^2}{2}=0,64\frac{mv^2}{2}\Rightarrow v=0,8v_0$$

Substituindo este dado na equação da conservação de quantidade de movimento (nossa primeira equação), encontramos:

$$mv_0=MV+mv\Rightarrow$$

$$mv_0=MV+m\cdot 0,8 \cdot v_0 \Rightarrow$$

$$V=\frac{mv_0}{5M}$$


Problema do looping não completo passando pelo centro

Deixe uma resposta

Qual é o valor da altura h, em função do raio da circunferência (loop), para que um corpo abandonado neste ponto inicie o loop e caia passando pelo centro deste mesmo loop? Despreze os atritos.

loopingcentro

Resolução:

Observe a figura abaixo. Nela acrescentamos uma nova variável \(\theta\).

looping

Com isso, pela conservação da energia, obtemos a relação à seguir:

$$mgh=mgr(1+\rm{sen}\theta)+\frac{mv^2}{2}\Rightarrow $$
$$\rm{v}^2=2g[h-R(1+\rm{sen}\theta)]\:\rm{eq.}01$$

Fazendo um diagrama de forças para o corpo no ponto onde ele perde o contato com o looping, isto é, quando a normal sobre o corpo é zero, teremos que \( P_y \) é a resultante centrípeta:

$$P_y=P \rm{cos} \alpha$$

Sendo \(\alpha= 90^o – \theta\) o ângulo em relação à horizontal da reta tangente (medido no sentido anti-horário), assim \( \rm{sen}\theta=\rm{cos}\theta\) e portanto \(P_y=P \rm{sen} \theta\). Portanto:
$$P\rm{sen}\theta=\frac{mv^2}{R}$$

Substituindo a equação obtida anteriormente para a velocidade, temos:
$$mg\rm{sen}\theta=\frac{m}{R} 2g[h-R(1+\rm{sen}\theta)]$$

Dividindo a equação inteira por \(mg\), multiplicando por \(R\) e desenvolvendo a distributiva:
$$R\rm{sen}\theta=2h-2R-2R\rm{sen}\theta\Rightarrow$$
$$\rm{sen}\theta=\frac{2}{3}\cdot\frac{h-R}{R}$$

Com isso podemos obter co-seno de \(\theta\):

$$\rm{cos}^2\theta=\sqrt{1-\rm{sen}^2\theta}$$

Desenvolvendo, obtemos:

$$\rm{cos}\theta=\frac{\sqrt{5R^2-4h^2+8hR}}{3R}$$

Agora vem uma sacada (foi uma sugestão de um aluno, o Rafael, da turma Ita, 2014), que achei muito boa. Vou resolver assim, e se alguém quiser tentar de outro jeito, fique a vontade.

Observe a figura abaixo. Se no ponto em que o corpo perde o contato com o looping ele “magicamente” não sofresse influência da gravidade e atravessasse o looping em linha reta, ele atingiria um alvo fictício no ponto onde está indicado o ângulo \(\theta\) que chamaremos de objeto \(O\). Agora, em uma situação análoga, voltando instante em que o corpo perde contato com o looping, com influência da gravidade, imagine que o ponto \(O\) inicie uma queda livre. É uma consequência, que não abordarei em detalhes aqui mas que vale a pena perguntar o seu professor se não entender, o fato de que o objeto atingirá o alvo \(O\) no centro da circunferência!

Com isso, a partir da figura abaixo, temos um novo triângulo retângulo em que o cateto oposto ao \(\theta\) é \(R\), a hipotenusa será \(\frac{gt^2}{2}\) e o cateto adjacente será \(v\dot t\).

loopingCom isso, podemos escrever:

 

$$ \left\{\begin{matrix}
\rm{sen}\theta =\frac{2R}{gt^2}\\
\rm{cos}\theta= \frac{2v}{gt}
\end{matrix}\right.$$

Dividindo \(\rm{sen}\theta\) por \(\rm{cos}^2\theta\), obtemos:

$$\frac{\rm{sen}\theta}{\rm{cos}^2\theta}=\frac{2R}{gt^2}\cdot \frac{g^2t^2}{4v^2}=\frac{Rg}{2v^2}$$

Substituindo a equação 01 (\(\rm{v}^2=2g[h-R(1+\rm{sen}\theta)]\)) e seno e co-seno de \(\theta\) encontrado acima, obtemos:

$$\frac{\rm{sen}\theta}{\rm{cos}^2\theta}=\frac{Rg}{4g[h-R(1+\rm{sen}\theta)]}\Rightarrow\\
\frac{2(h-R)}{3R}\cdot\frac{9R^2}{5R^2-4h^2+8hR}=\frac{R}{4[h-R(1+\rm{sen}\theta)]}\Rightarrow\\
2(h-R)\cdot\frac{3}{5R^2-4h^2+8hR}=\frac{1}{4[h-R(1+\rm{sen}\theta)]}$$

Substituindo \(\rm{sen}\theta\):

$$2(h-R)\cdot\frac{3}{5R^2-4h^2+8hR}=\frac{1}{4[h-R(1+\frac{2(h-R)}{3R})]}\Rightarrow\\
\frac{2(h-R)}{5R^2-4h^2+8hR}=\frac{1}{4[3h-3R-2(h-R)]}\Rightarrow\\
\frac{2(h-R)}{5R^2-4h^2+8hR}=\frac{1}{4[3h-3R-2h+2R)]}\Rightarrow\\
\frac{2(h-R)}{5R^2-4h^2+8hR}=\frac{1}{4[h-R]}\Rightarrow\\
\frac{8(h-R)^2}{5R^2-4h^2+8hR}=1\Rightarrow\\
8(h-R)^2=5R^2-4h^2+8hR\Rightarrow\\
8(h^2-2hR+R^2)=5R^2-4h^2+8hR\Rightarrow\\
8h^2-16hR+8R^2=5R^2-4h^2+8hR\Rightarrow\\
12\cdot h^2-24R\cdot h+3R^2=0$$

Resolvendo por Bhaskara:

$$\Delta=b^2-4ac\Rightarrow\\
\Delta=(24R)^2-4\cdot 12\cdot 3R^2\Rightarrow\\
\Delta=576\cdot R^2-144R^2\Rightarrow\\
\Delta=432R^2\Rightarrow\\
\Delta=3(12R)^2$$

Assim:

$$x=\frac{-b\pm \sqrt\Delta}{2a}\Rightarrow\\
x=\frac{24R\pm 12R\sqrt3}{24}\Rightarrow\\
x=\frac{2R\pm R\sqrt3}{2}\Rightarrow\\
x=\frac{R}{2}\cdot \left ( 2\pm \sqrt{3} \right )$$

Isso nos da duas raízes. Uma porém é inválida. Resta saber qual e porque.

Temos que considerar a maior raiz, pois \( x>R\) (veja que o lançamento só é possível se a altura do ponto em que o corpo perde contato for acima do ponto no centro do looping). Logo, como \(x=\frac{R}{2}\cdot \left ( 2 – \sqrt{3} \right ) < R\) , esta raiz não satisfaz nossas condições.

Assim a resposta será:

$$x=\frac{R}{2}\cdot \left ( 2 + \sqrt{3} \right )$$