Qual é o valor da altura h, em função do raio da circunferência (loop), para que um corpo abandonado neste ponto inicie o loop e caia passando pelo centro deste mesmo loop? Despreze os atritos.

Resolução:

Observe a figura abaixo. Nela acrescentamos uma nova variável \(\theta\).

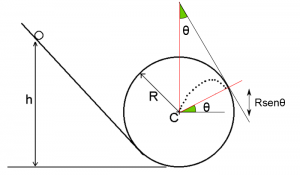
Com isso, pela conservação da energia, obtemos a relação à seguir:

$$mgh=mgr(1+\rm{sen}\theta)+\frac{mv^2}{2}\Rightarrow $$
$$\rm{v}^2=2g[h-R(1+\rm{sen}\theta)]\:\rm{eq.}01$$

Fazendo um diagrama de forças para o corpo no ponto onde ele perde o contato com o looping, isto é, quando a normal sobre o corpo é zero, teremos que \( P_y \) é a resultante centrípeta:

$$P_y=P \rm{cos} \alpha$$

Sendo \(\alpha= 90^o – \theta\) o ângulo em relação à horizontal da reta tangente (medido no sentido anti-horário), assim \( \rm{sen}\theta=\rm{cos}\theta\) e portanto \(P_y=P \rm{sen} \theta\). Portanto:
$$P\rm{sen}\theta=\frac{mv^2}{R}$$

Substituindo a equação obtida anteriormente para a velocidade, temos:
$$mg\rm{sen}\theta=\frac{m}{R} 2g[h-R(1+\rm{sen}\theta)]$$

Dividindo a equação inteira por \(mg\), multiplicando por \(R\) e desenvolvendo a distributiva:
$$R\rm{sen}\theta=2h-2R-2R\rm{sen}\theta\Rightarrow$$
$$\rm{sen}\theta=\frac{2}{3}\cdot\frac{h-R}{R}$$

Com isso podemos obter co-seno de \(\theta\):

$$\rm{cos}^2\theta=\sqrt{1-\rm{sen}^2\theta}$$

Desenvolvendo, obtemos:

$$\rm{cos}\theta=\frac{\sqrt{5R^2-4h^2+8hR}}{3R}$$

Agora vem uma sacada (foi uma sugestão de um aluno, o Rafael, da turma Ita, 2014), que achei muito boa. Vou resolver assim, e se alguém quiser tentar de outro jeito, fique a vontade.

Observe a figura abaixo. Se no ponto em que o corpo perde o contato com o looping ele “magicamente” não sofresse influência da gravidade e atravessasse o looping em linha reta, ele atingiria um alvo fictício no ponto onde está indicado o ângulo \(\theta\) que chamaremos de objeto \(O\). Agora, em uma situação análoga, voltando instante em que o corpo perde contato com o looping, com influência da gravidade, imagine que o ponto \(O\) inicie uma queda livre. É uma consequência, que não abordarei em detalhes aqui mas que vale a pena perguntar o seu professor se não entender, o fato de que o objeto atingirá o alvo \(O\) no centro da circunferência!

Com isso, a partir da figura abaixo, temos um novo triângulo retângulo em que o cateto oposto ao \(\theta\) é \(R\), a hipotenusa será \(\frac{gt^2}{2}\) e o cateto adjacente será \(v\dot t\).

Com isso, podemos escrever:

 

$$ \left\{\begin{matrix}
\rm{sen}\theta =\frac{2R}{gt^2}\\
\rm{cos}\theta= \frac{2v}{gt}
\end{matrix}\right.$$

Dividindo \(\rm{sen}\theta\) por \(\rm{cos}^2\theta\), obtemos:

$$\frac{\rm{sen}\theta}{\rm{cos}^2\theta}=\frac{2R}{gt^2}\cdot \frac{g^2t^2}{4v^2}=\frac{Rg}{2v^2}$$

Substituindo a equação 01 (\(\rm{v}^2=2g[h-R(1+\rm{sen}\theta)]\)) e seno e co-seno de \(\theta\) encontrado acima, obtemos:

$$\frac{\rm{sen}\theta}{\rm{cos}^2\theta}=\frac{Rg}{4g[h-R(1+\rm{sen}\theta)]}\Rightarrow\\
\frac{2(h-R)}{3R}\cdot\frac{9R^2}{5R^2-4h^2+8hR}=\frac{R}{4[h-R(1+\rm{sen}\theta)]}\Rightarrow\\
2(h-R)\cdot\frac{3}{5R^2-4h^2+8hR}=\frac{1}{4[h-R(1+\rm{sen}\theta)]}$$

Substituindo \(\rm{sen}\theta\):

$$2(h-R)\cdot\frac{3}{5R^2-4h^2+8hR}=\frac{1}{4[h-R(1+\frac{2(h-R)}{3R})]}\Rightarrow\\
\frac{2(h-R)}{5R^2-4h^2+8hR}=\frac{1}{4[3h-3R-2(h-R)]}\Rightarrow\\
\frac{2(h-R)}{5R^2-4h^2+8hR}=\frac{1}{4[3h-3R-2h+2R)]}\Rightarrow\\
\frac{2(h-R)}{5R^2-4h^2+8hR}=\frac{1}{4[h-R]}\Rightarrow\\
\frac{8(h-R)^2}{5R^2-4h^2+8hR}=1\Rightarrow\\
8(h-R)^2=5R^2-4h^2+8hR\Rightarrow\\
8(h^2-2hR+R^2)=5R^2-4h^2+8hR\Rightarrow\\
8h^2-16hR+8R^2=5R^2-4h^2+8hR\Rightarrow\\
12\cdot h^2-24R\cdot h+3R^2=0$$

Resolvendo por Bhaskara:

$$\Delta=b^2-4ac\Rightarrow\\
\Delta=(24R)^2-4\cdot 12\cdot 3R^2\Rightarrow\\
\Delta=576\cdot R^2-144R^2\Rightarrow\\
\Delta=432R^2\Rightarrow\\
\Delta=3(12R)^2$$

Assim:

$$x=\frac{-b\pm \sqrt\Delta}{2a}\Rightarrow\\
x=\frac{24R\pm 12R\sqrt3}{24}\Rightarrow\\
x=\frac{2R\pm R\sqrt3}{2}\Rightarrow\\
x=\frac{R}{2}\cdot \left ( 2\pm \sqrt{3} \right )$$

Isso nos da duas raízes. Uma porém é inválida. Resta saber qual e porque.

Temos que considerar a maior raiz, pois \( x>R\) (veja que o lançamento só é possível se a altura do ponto em que o corpo perde contato for acima do ponto no centro do looping). Logo, como \(x=\frac{R}{2}\cdot \left ( 2 – \sqrt{3} \right ) < R\) , esta raiz não satisfaz nossas condições.

Assim a resposta será:

$$x=\frac{R}{2}\cdot \left ( 2 + \sqrt{3} \right )$$