Como motivação inicial, comecemos com um exercício:
Uma esfera é lançada horizontalmente de uma altura igual à 19,6 m num local onde a aceleração da gravidade vale 9,8 m/s2 e colide de forma parcialmente elástica tal que e = 0,8. Construa o gráfico da velocidade versus tempo e da altura versus tempo.
Lembrando que o coeficiente de restituição, para uma colisão unidimensional, considerando o sinal da velocidade (isto é, as velocidades das partículas podem ser positivas ou negativas) é dado por:
$$e=\frac{v_B’-v_A’}{v_A-v_B}$$
Sendo vA a velocidade do corpo A antes da colisão, Sendo vB a velocidade do corpo B antes da colisão, Sendo vA‘ a velocidade do corpo A após a colisão e Sendo vB‘ a velocidade de b após a colisão, conforme desenho abaixo.
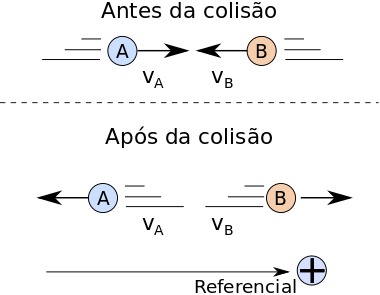
A velocidade possui sinal que depende do referencial. O esquema acima é somente ilustrativo, uma vez que após a colisão, a esfera A poderia estar indo para a direita, por exemplo, ou a B poderia se mover para a esuerda. O que importa é usar as duas equações: conservação da queantidade de movimento e conservação da quantidade de movimento.
Além da equação do coeficiente de restituição, precisamos escrever que a quantidade de movimento se conserva, isto é:
$$\Sigma Q_{inicio}=\Sigma Q_{final}\Rightarrow$$
$$Q_A+Q_B=Q_A’+Q_B’\Rightarrow$$
$$m_A\cdot v_A+m_B\cdot v_B=m_A\cdot v_A’+m_B\cdot v_B’$$
Tente resolver e verificar se esta simulação está legal.
Acesse o link abaixo para interagir.
https://www.glowscript.org/#/user/djkcond/folder/Mecanica/program/ColisaoComSolo
SIMULAÇÃO REMOVIDA DO CORPO DESTE BLOG PARA NÃO PREJUDICAR A FORMATAÇÃO: clique no link apresentado para ir para a página onde se encontra a simulação.