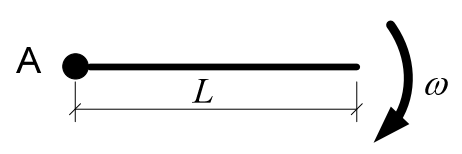Observação 1: as respostas estão com a mesma cor de fundo, então para saber a resposta basta selecionar a linha escrito “RESPOSTA”.
Observação 2: eu pretendia montar a resolução da prova apenas de física, mas disponibilizar toda a prova aqui, com o gabarito abaixo da questão. Fiquei doente por uma semana e disponibilizar toda a resolução agora, depois da segunda fase, não faz mais sentido (iria disponibilizar para meus alunos), por essa razão, vou deixar disponível aqui apenas as resoluções que já havia feito e deixarei disponível apenas a prova de física e química digitada no blog.
Observação 3: você pode baixar a PROVA e o GABARITO. A prova da segunda fase você encontra aqui: (Matemática, Física, Química, Português/Inglês) e o gabarito da prova de Português/Ingles.
Observação 4: uma resolução mais completa você encontra em https://imeresolve.wordpress.com/category/vestibular-ime-201516/
QUESTÕES DE 1 A 15
MATEMÁTICA
1$^a$ QUESTÃO
Dados três conjuntos quaisquer F, G e H. O conjunto G – H é igual ao conjunto:
(A) $(G \cup F) – (F – H)$
(B) $(G \cup H) – (H – F)$
(C) $(G \cup (H – F)) \cap \overline H $
(D) $\overline G \cup ( H \cap F)$
(E) $(\overline H \cap G) \cap (G – F )$
RESPOSTA: C
2$^a$ QUESTÃO
O polinômio �$x^3+ax^2+bx+c$ tem raízes reais �$\alpha$,$-\alpha$� e � � $\frac 1 \alpha$. Portanto o valor da soma � $b+c^2+ac+\frac b c^2$ � � é:
(A) −2
(B) −1
(C) 0
(D) 1
(E) 2
RESPOSTA: A
3$^a$ QUESTÃO
Sabendo-se que $m$ e $n$ são inteiros positivos tais que $3^m + 14400 = n^2$, determine o resto da divisão de $m+n$ por 5.
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
RESPOSTA: E
4$^a$ QUESTÃO
O valor do somatório abaixo é: $$\sum_{k=1}^{15} \rm{Img} \left ( cis^{2k-1}\frac {\pi} {36} \right )$$
(A) $\frac{2+ \sqrt 3}{4 \rm{sen} \frac {\pi}{36}}$
(B) $\frac{2- \sqrt 3}{4 \rm{sen} \frac {\pi}{36}}$
(C) $\frac{1}{4 \rm{sen} \frac {\pi}{36}}$
(D) $ \rm{sen} \frac {\pi}{36}$
(E) $\frac 1 4$
Observação: $\rm{Img}(w)$ é a parte imaginária de $w$.
RESPOSTA: A
5$^a$ QUESTÃO
Seja $P(�x)� = x^2� + a�x + b$�. Sabe-se que $P(x)$ e $P(P(P(x)))$ têm uma raiz em comum. Pode-se afirmar que para todo valor $a$ e $b$
(A) $P(−1)P(���1�) < 0$
(B) $P(��−1)P(���1)� = 0$
(C) $P(��−1)� + P(��1)� = 2$
(D) $P(0)P(1)� = 0$
(E) $P(0) + P(1)� = 0$
RESPOSTA: D
6$^a$ QUESTÃO
Sabendo-se que os números reais positivos $a$, $b$ e $c$ formam uma progressão geométrica e $\rm{log} \left ( \frac{5c}{a} \right )$, $\rm{log} \left( \frac{3b}{5c} \right )$ e $\rm{log} \left ( \frac{a}{3b} \right )$ formam uma progressão aritmética, ambas nessa ordem, então pode-se afirmar que $a$, $b$ e $c$
(A) formam os lados de um triângulo obtusângulo.
(B) formam os lados de um triângulo acutângulo não equilátero.
(C) formam os lados de um triângulo equilátero.
(D) formam os lados de um triângulo retângulo.
(E) não podem formar os lados de um triângulo.
RESPOSTA: E
7$^a$ QUESTÃO
O valor da soma abaixo é:
$$\binom{2016}{5}+ \binom{2017}{5}+ \binom{2018}{5}+ \binom{2019}{5} + \binom{2020}{5}+ \binom{2016}{5}$$
(A) $\binom{2020}{6}$
(B) $\binom{2020}{7}$
(C) $\binom{2021}{5}$
(D) $\binom{2021}{6}$
(E) $\binom{2022}{5}$
RESPOSTA: D
8$^a$ QUESTÃO
Os inteiros � $n$ e $m$� são sorteados do conjunto $\left \{1,2,3,…,2016 \right \}$, podendo haver repetição. Qual a probabilidade do produto $ n \times m$�� ser múltiplo de 12?
(A) $\frac{5}{12}$
(B) $\frac{5}{18}$
(C) $\frac{5}{24}$
(D) $\frac{5}{36}$
(E) �$\frac{5}{144}$
RESPOSTA: B
9$^a$ QUESTÃO
Seja $A=\begin{bmatrix} a & b \\ -b & a \end{bmatrix}$. O maior valor de $a$, com $a \neq 1$, que satisfaz $A^{24}= I$:
(A) $\frac 1 2 $
(B) $\frac{\sqrt{2}}{2}$
(C) $\frac{\sqrt{3}}{2}$
(D) $\frac{\sqrt{2}}{4} \left ( \sqrt{3} -1 \right )$
(E) $\frac{\sqrt{2}}{4} \left ( \sqrt 3 + 1 \right )$
Observação: $I$ é a matriz identidade $2 \times 2$.
RESPOSTA: E
10$^a$ QUESTÃO
Quantos inteiros $k$ satisfazem à desigualdade $2\sqrt{\rm{log}_{10}k-1}+10\rm{log}_{10^{-1}} \; k^{1/4}+3>0$?
(A) 10
(B) 89
(C) 90
(D) 99
(E) 100
RESPOSTA: C
11$^a$ QUESTÃO
Seja a equação $\frac{\rm{sen}(2x)}{\rm{tg}x}=\frac 1 2 \ $. As soluções dessa equação para $x \in \left [ -\frac{\pi}{2}, \pi \right ]$, formam um polígono no círculo trigonométrico de área
(A) $\frac {\sqrt{3}} {2}$
(B) $\sqrt 3$
(C) $\frac{5 \sqrt 3}{8}$
(D) $\frac 1 2$
(E) $1$
RESPOSTA: A
12$^a$ QUESTÃO
O lugar geométrico dos pontos em $\mathbb{R}^2$� equidistantes às retas de equações $$ 4x + 3y – 2 = 0 \; \; \rm{e} \; \; 12x – 16 y + 5 = 0$$
é
(A) $4x + 28 y + 13 = 0$
(B) $8x – 7y – 13 = 0$
(C) $28 x – 4y – 3 = 0$
(D) $56x^2 + 388xy – 184x – 56y^2 – 16y + 19 =0$
(E) $112x^2 + 768xy – 376x – 112y^2 – 32y + 39 =0$
RESPOSTA: E
13$^a$ QUESTÃO
Considere quatro pontos distintos coplanares. Das distâncias entre esses pontos, quatro delas valem a e duas delas valem b. O valor máximo da relação �$ \left ( \frac{a}{b} \right ) ^2 $ é
(A) 2
(B) $ 1+\sqrt3$
(C) $2+\sqrt3$
(D) $1+2 \sqrt2$
(E)$2+2sqrt3$
RESPOSTA: C
14$^a$ QUESTÃO
Em um triângulo ABC, o ponto D é o pé da bissetriz relativa ao ângulo Â. Sabe-se que
$$ \overline{AC}=\overline{AD}, \; r=\frac{\overline{AB}}{\overline{AC}} \; \rm{e} \; \rm{que} \; \hat{C}=\alpha $$
Portanto o valor de $\rm{sen}^2\alpha$ é
(A) $\frac{3r-1}{4}$
(B) $\frac{3r-1}{4r}$
(C) $\frac{r+3}{4}$
(D) $\frac{3r+1}{4r}$
(E) $\frac{3r+1}{4}$
RESPOSTA: D
15$^a$ QUESTÃO
Sejam dois quadrados de lado a situados em planos distintos que são paralelos entre si e situados a uma distância d, um do outro. A reta que liga os centros dos quadrados é perpendicular a esses planos. Cada diagonal de um quadrado é paralela a dois lados do outro quadrado. Liga-se cada vértice de cada quadrado aos dois vértices mais próximos do outro quadrado. Obtêm-se, assim, triângulos que, conjuntamente com os quadrados, formam um sólido S. Qual a distância entre estes planos distintos em função de a, de modo que os triângulos descritos acima sejam equiláteros?
(A) $\frac{a}{2}$
(B) $\frac{a\sqrt3}{2}$
(C) $\frac{a\sqrt{10}}{8}$
(D) $\frac{a\sqrt[4]{8}}{2}$
(E) $\frac{a(4-3\sqrt2)}{2}$
RESPOSTA: D
QUESTÕES DE 16 A 30
FÍSICA
16$^a$ QUESTÃO
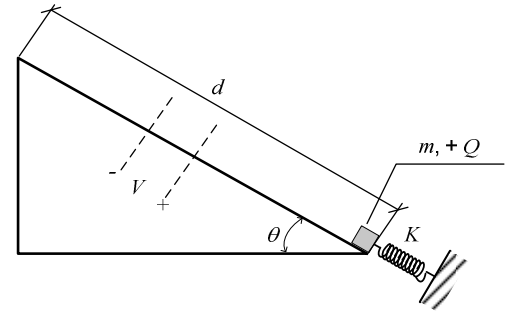
Um corpo de carga positiva, inicialmente em repouso sobre uma rampa plana isolante com atrito, está apoiado em uma mola, comprimindo-a. Após ser liberado, o corpo entra em movimento e atravessa uma região do espaço com diferença de potencial V, sendo acelerado. Para que o corpo chegue ao final da rampa com velocidade nula, a distância d indicada na figura é
Dados:
- deformação inicial da mola comprimida: x;
- massa do corpo: m;
- carga do corpo: + Q;
- aceleração da gravidade: g;
- coeficiente de atrito dinâmico entre o corpo e a rampa: $\mu$;
- ângulo de inclinação da rampa: $\theta$;
- constante elástica da mola: K.
Considerações:
- despreze os efeitos de borda;
- a carga do corpo permanece constante ao longo da trajetória.
(A) $\frac{Kx^2+2QV}{2(1+\mu)mg\rm{sen}\theta}$
(B) $\frac{Kx^2+QV}{2(1+\mu)mg\rm{sen}\theta}$
(C) $\frac{\frac{Kx^2}{2}+QV}{2(1+\mu)mg\rm{cos}\theta}$
(D) $\frac{Kx^2-2QV}{2mg(\rm{sen}\theta +\mu \rm{cos}\theta)}$
(E) $\frac{Kx^2+2QV}{2mg(\rm{sen}\theta +\mu \rm{cos}\theta)}$
RESPOSTA: E
RESOLUÇÃO

17$^a$ QUESTÃO
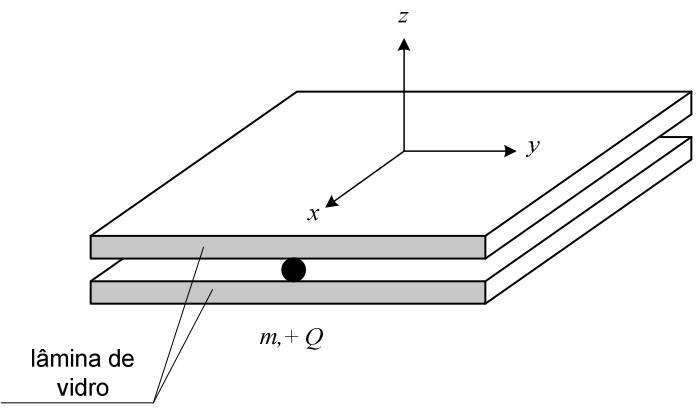
Uma partícula de massa m e carga + Q encontra-se confinada no plano XY entre duas lâminas infinitas de vidro, movimentando-se sem atrito com vetor velocidade (v,0,0) no instante t = 0, quando um dispositivo externo passa a gerar um campo magnético dependente do tempo, cujo vetor é (f(t),f(t),B), onde B é uma constante. Pode-se afirmar que a força normal exercida sobre as lâminas é nula quando t é
Consideração:
- desconsidere o efeito gravitacional.
(A) $\left ( \frac{m}{QB} \right ) \frac{\pi}{8}$
(B) $\left ( \frac{m}{QB} \right ) \frac{\pi}{4}$
(C) $\left ( \frac{m}{QB} \right ) \frac{\pi}{2}$
(D) $\left ( \frac{m}{QB} \right )\pi$
(E) $ 2 \left ( \frac{m}{QB} \right ) \pi$
RESPOSTA: B
RESOLUÇÃO


18$^a$ QUESTÃO
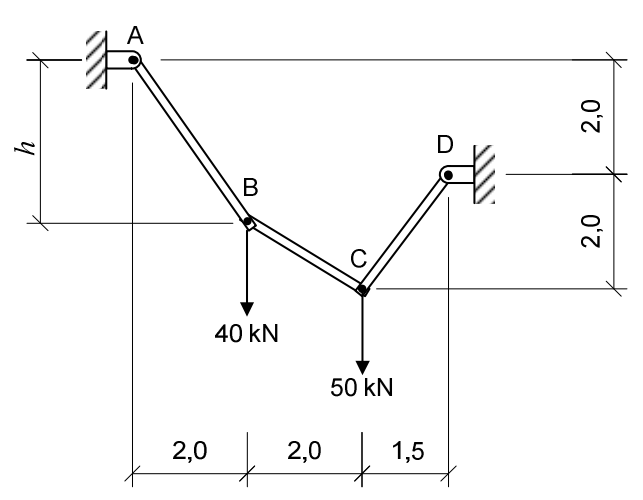
A figura acima, cujas cotas estão em metros, exibe uma estrutura em equilíbrio formada por três barras rotuladas AB, BC e CD. Nos pontos B e C existem cargas concentradas verticais. A maior força de tração que ocorre em uma barra, em kN, e a altura h, em metros, da estrutura são
Consideração:
- as barras são rígidas, homogêneas, inextensíveis e de pesos desprezíveis.
(A) 50,0 e 2,50
(B) 31,6 e 1,67
(C) 58,3 e 3,33
(D) 50,0 e 1,67
(E) 58,3 e 2,50
RESPOSTA: C
19$^a$ QUESTÃO
Uma fonte sonora está situada no ponto de coordenadas x = 0 m e y = 0 m e outra no ponto de coordenadas x = 0 m e y = 4 m. As ondas produzidas pelas duas fontes têm a mesma frequência e estão em fase. Um observador situado no ponto de coordenadas x = 3 m e y = 0 m nota que a intensidade do som diminui quando ele se move paralelamente ao eixo y no sentido positivo ou no sentido negativo. Se a velocidade do som no local é 340 m/s, a menor frequência das fontes, em Hz, que pode explicar essa observação é
(A) 85
(B) 170
(C) 340
(D) 680
(E) 1360
RESPOSTA: B
RESOLUÇÃO

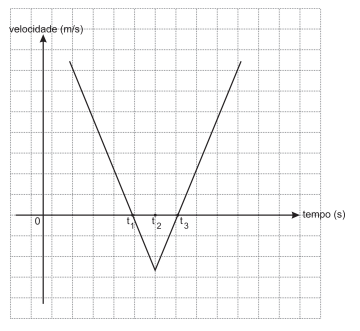
20$^a$ QUESTÃO
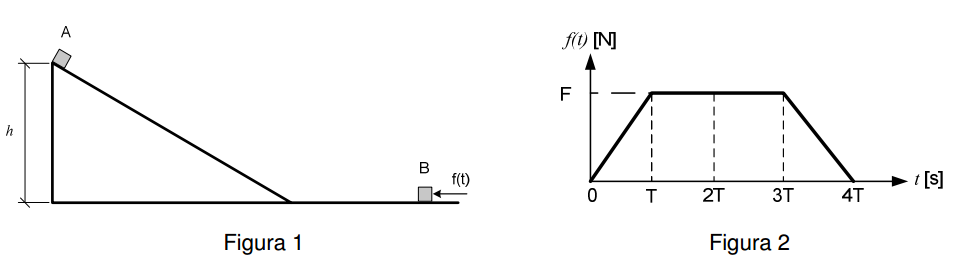
Na Figura 1, o corpo A, constituído de gelo, possui massa m e é solto em uma rampa a uma altura h. Enquanto desliza pela rampa, ele derrete e alcança o plano horizontal com metade da energia mecânica e metade da massa iniciais. Após atingir o plano horizontal, o corpo A se choca, no instante 4T, com o corpo B, de massa m, que foi retirado do repouso através da aplicação da força $f(t)$, cujo gráfico é exibido na Figura 2.
Para que os corpos parem no momento do choque, F deve ser dado por
Dado:
- aceleração da gravidade: g.
Observações:
- o choque entre os corpos é perfeitamente inelástico;
- o corpo não perde massa ao longo de seu movimento no plano horizontal.
(A) $\frac{m\sqrt{2gh}}{8T}$
(B) $\frac{m\sqrt{2gh}}{6T}$
(C) $\frac{m\sqrt{2gh}}{4T}$
(D) $\frac{m\sqrt{2gh}}{3T}$
(E) $\frac{m\sqrt{2gh}}{2T}$
RESPOSTA: B
RESOLUÇÃO
21$^a$ QUESTÃO
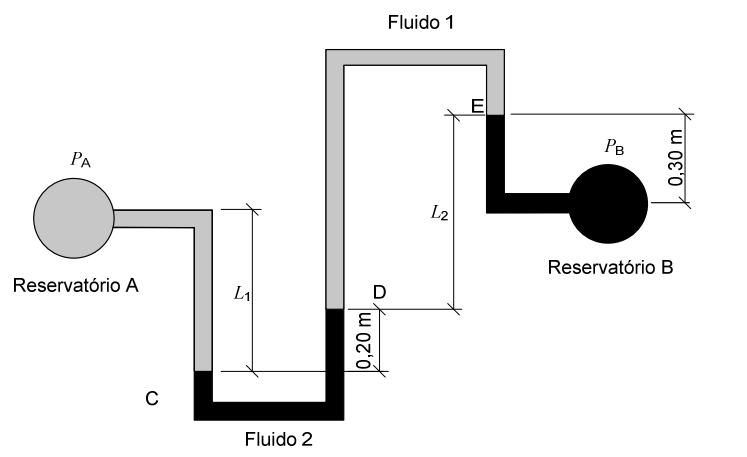
Considerando o esquema acima, um pesquisador faz três afirmações que se encontram listadas a seguir:
Afirmação I. Se a diferença de pressão entre os dois reservatórios ($P_A – P_B$) for equivalente a 20 mm de coluna de água, a variação de massa específica entre os dois fluidos ($\rho_1 – \rho_2$) é igual a 0,2 kg/L.
Afirmação II. Se o Fluido 1 for água e se a diferença de pressão ($P_A – P_B$) for de 0,3 kPa, a massa específica do Fluido 2 é igual a 0,7 kg/L.
Afirmação III. Caso o Fluido 1 tenha massa específica igual à metade da massa específica da água, o Fluido 3 (que substitui o Fluido 2 da configuração original) deve ser mais denso do que a água para que a diferença de pressão entre os reservatórios seja a mesma da afirmação I.
Está(ão) correta(s) a(s) afirmação(ões)
Dados:
- massa específica da água: 1 kg/L;
- aceleração da gravidade: 10 m/s$^2$ ;
- Para as afirmações I e II: $L_1 = 0,30$ m e $L_2 = 0,40$ m;
- Para a afirmação III apenas: $L_1 = 0,60$ m e $L_2 = 0,80$ m.
Consideração:
- os fluidos são imiscíveis.
(A) I apenas.
(B) II apenas.
(C) III apenas.
(D) I e II apenas.
(E) I, II e III.
RESPOSTA: D
22$^a$ QUESTÃO
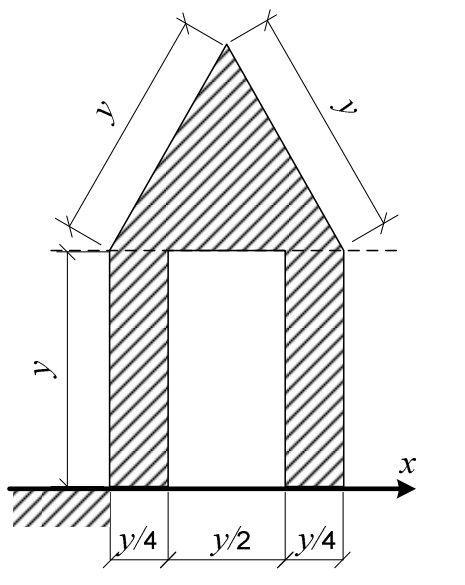
Um corpo rígido e homogêneo apresenta seção reta com dimensões representadas na figura acima. Considere que uma força horizontal $F$, paralela ao eixo $x$, é aplicada sobre o corpo a uma distância de 1,5 u.c. do solo e que o corpo desliza sem atrito pelo solo plano horizontal. Para que as duas reações do solo sobre a base do corpo sejam iguais, a distância $y$, em u.c., deverá ser
Consideração:
- u.c. – unidade de comprimento.
(A) $cos(\pi/3)$
(B) $\rm{sen}(\pi/3)$
(C) $2cos(\pi/3)$
(D) $2\rm{sen}(\pi/3)$
(E) $3cos(\pi/3)$
RESPOSTA: D
RESOLUÇÃO

23$^a$ QUESTÃO
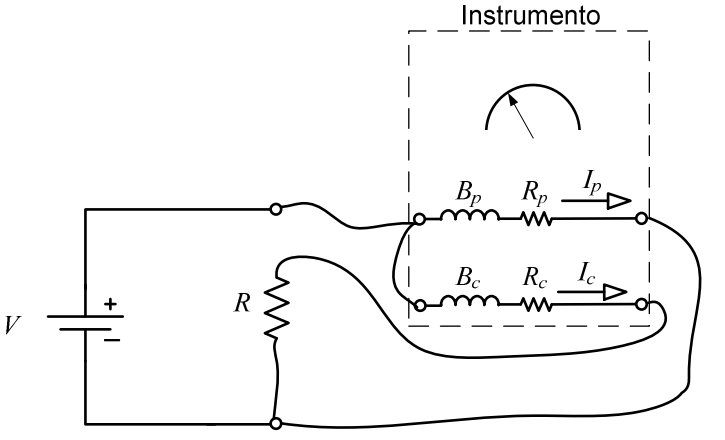
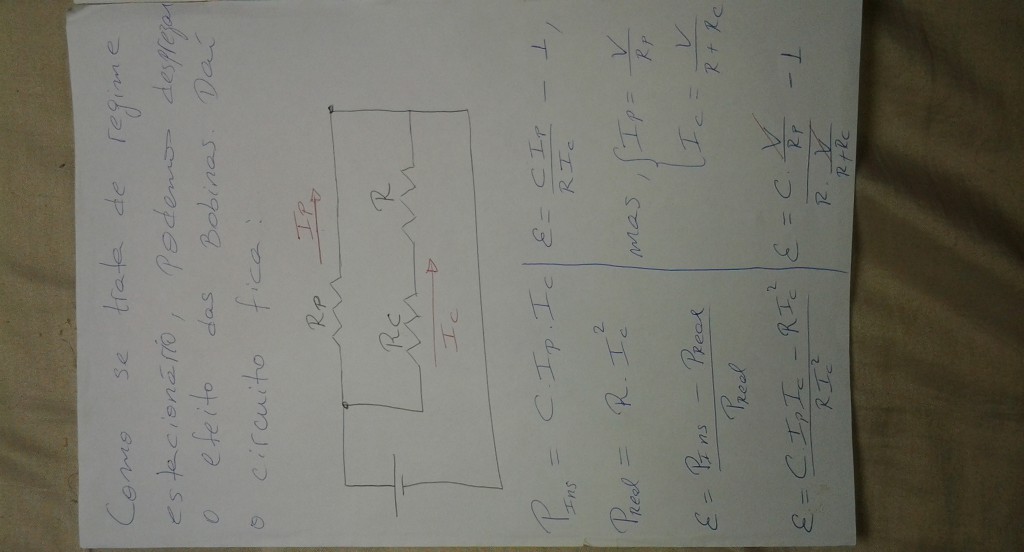
A figura acima apresenta o esquema de ligação de um instrumento usado para medir a potência fornecida a uma carga. Sabe-se que a leitura de potência do instrumento em regime permanente é $P_{instrumento} = C \cdot I_p \cdot I_c$ e que o erro relativo é $\varepsilon =\frac{P_{instrumento} -P_{real}}{P_{real}}$. Diante do exposto, o valor da resistência $R_p$ do instrumento deve ser igual a
Dados:
- potência medida na resistência $R$ empregando-se o instrumento: $P_{instrumento}$;
- potência real dissipada na resistência $R$: $P_{real}$;
- constante do instrumento: $C$;
- tensão de alimentação do circuito: $V$;
- corrente da bobina de potencial ($B_p$): $I_p$;
- corrente da bobina de corrente ($B_c$): $I_c$.
Considerações:
- $R\ll r_p$; e
- $R \gg R_c$.
(A) $\frac{C}{\varepsilon}$
(B) $\frac{2C}{\varepsilon}$
(C) $\frac{C}{1+\varepsilon}$
(D) $\frac{C}{1-\varepsilon}$
(E) $\frac{C}{2(1+\varepsilon)}$
RESPOSTA: C
RESOLUÇÃO

24$^a$ QUESTÃO
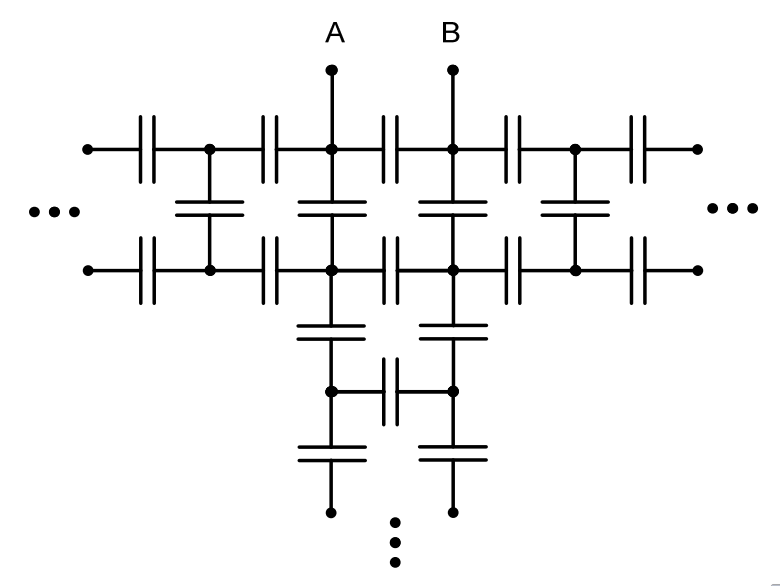
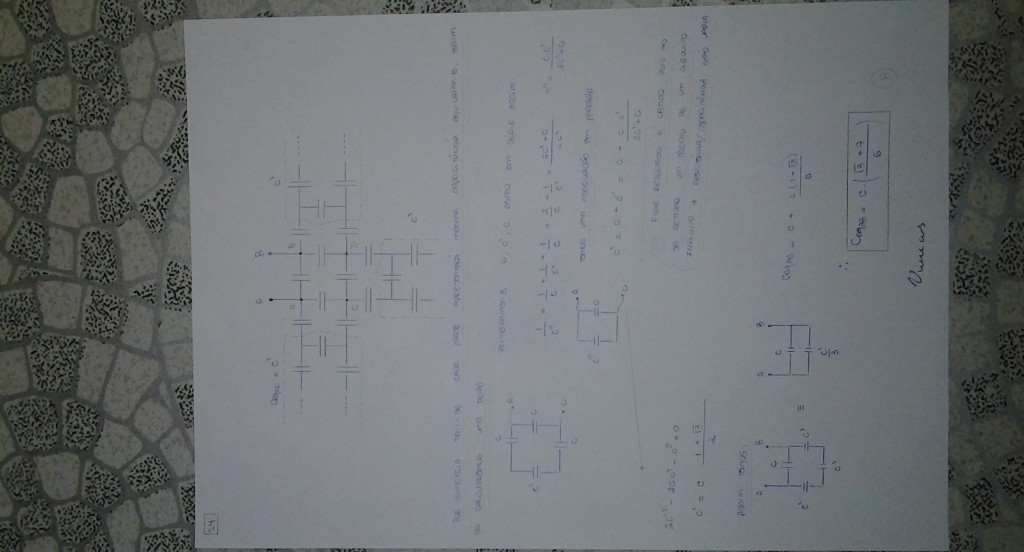
Um circuito é composto por capacitores de mesmo valor $C$ e organizado em três malhas infinitas. A capacitância equivalente vista pelos terminais A e B é
(A) $(3^{1/2}+7)\frac{C}{6}$
(B) $(3^{1/2}+1)\frac{C}{3}$
(C) $(3^{1/2}+1)\frac{C}{6}$
(D) $(3^{1/2}+5)\frac{C}{2}$
(E) $(3^{1/2}+1)\frac{C}{2}$
RESPOSTA: A
RESOLUÇÃO
25$^a$ QUESTÃO
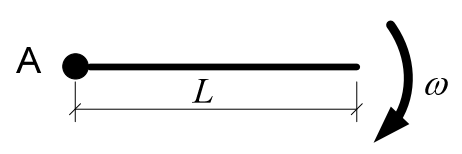
Uma corda de comprimento $L$ e densidade linear constante gira em um plano em torno da extremidade fixa no ponto A a uma velocidade angular constante igual a $\omega$. Um pulso ondulatório é gerado a partir de uma das extremidades. A velocidade $v$ do pulso, no referencial da corda, a uma distância $r$ da extremidade fixa é dada por
(A) $\omega \frac{L-r}{\sqrt2}$
(B) $\omega \sqrt{\frac{L(L-r)}{2}}$
(C) $\frac{\omega}{\sqrt2 L}(L^2-r^2)$
(D) $\omega \sqrt{\frac{L^2-r^2}{2}}$
(E) $\frac{\omega L}{\sqrt 2} \sqrt{\frac{L-r}{L+r}}$
RESPOSTA: D
RESOLUÇÃO

26$^a$ QUESTÃO
Dois observadores em movimento acompanham o deslocamento de uma partícula no plano. O observador 1, considerando estar no centro de seu sistema de coordenadas, verifica que a partícula descreve um movimento dado pelas equações $x_1(t) = 3cos(t)$ e $y_1(t) = 4\rm{sen}(t)$, sendo t a variável tempo. O observador 2, considerando estar no centro de seu sistema de coordenadas, equaciona o movimento da partícula como $x_2(t) = 5cos(t)$ e $y_2(t) = 5\rm{sen}(t)$. O observador 1 descreveria o movimento do observador 2 por meio da equação:
Observações:
- os eixos $x_1$ e $x_2$ são paralelos e possuem o mesmo sentido; e
- os eixos $y_1$ e $y_2$ são paralelos e possuem o mesmo sentido.
(A) $9x^2+16y^2=25$
(B) $\frac{x^2}{9}+\frac{y^2}{16}=25$
(C) $4x^2+y^2=1$
(D) $\frac{x^2}{4}+y^2=1$
(E) $4x^2+y^2=4$
RESPOSTA: D
RESOLUÇÃO

27$^a$ QUESTÃO
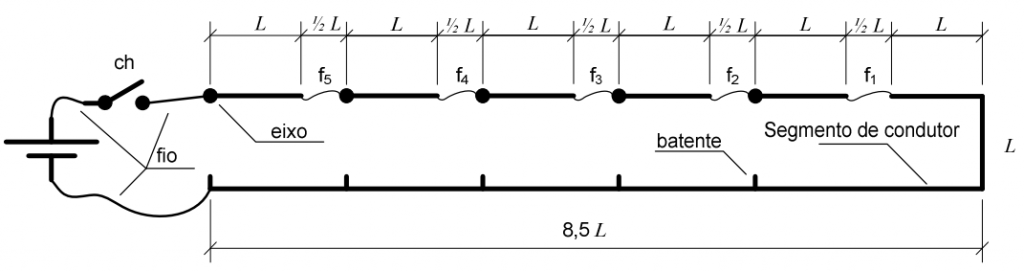
Um circuito é alimentado por uma bateria através de uma chave temporizada ch que após o seu fechamento, abrir-se-á depois de transcorrido um período de tempo igual a $T$. Esse circuito é formado por segmentos de condutores com a mesma seção, mesma resistividade e comprimentos indicados na figura. Também estão inseridos cinco fusíveis $f_1$ a $f_5$, que têm a função de manter a continuidade do fluxo de corrente e de manter os segmentos conectados. Sempre que um dos fusíveis queimar, o segmento imediatamente à esquerda vai girar no sentido horário, fechando o contato, através de um batente, após decorridos $T/4$. Sabe-se que cada fusível necessita de $T/4$ para se romper diante de uma corrente maior ou igual à corrente de ruptura. A partir do fechamento da chave temporizada ch até a sua abertura, a energia consumida pelo circuito é igual a
Dados:
- correntes de ruptura para cada fusível a partir da direita:
- o $f_1$: 0,9 $I$;
- o $f_2$: 1,1 $I$;
- o $f_3$: 1,5 $I$;
- o $f_4$: 1,8 $I$; e
- o $f_5$: 2,1 $I$.
- resistividade do segmento: $\rho$;
- seção do fio: $S$;
- diferença de potencial da bateria: $U$.
Observações:
- $I$ corresponde a corrente elétrica com todos os fusíveis ligados;
- desconsidere a resistência dos fusíveis, da chave, dos fios e dos engates que conectam a fonte ao circuito.
(A) $\left ( \frac{1}{24}+\frac{1}{20}\right ) \frac{U^2ST}{\rho L}$
(B) $\left ( \frac{1}{34}+\frac{1}{24}\right ) \frac{U^2ST}{\rho L}$
(C) $\left ( \frac{1}{42}+\frac{1}{34}\right ) \frac{U^2ST}{\rho L}$
(D) $\left ( \frac{1}{62}+\frac{1}{44}\right ) \frac{U^2ST}{\rho L}$
(E) $\left ( \frac{1}{62}+\frac{1}{22}\right ) \frac{U^2ST}{\rho L}$
RESPOSTA: D
28$^a$ QUESTÃO
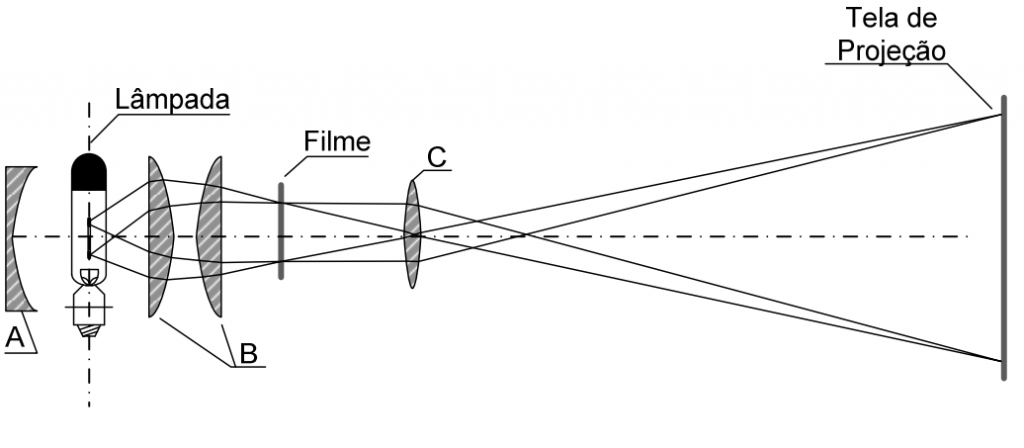
A figura acima apresenta um desenho esquemático de um projetor de imagens, onde A é um espelho e B e C são lentes. Com relação aos elementos do aparelho e à imagem formada, pode-se afirmar que
(A) o espelho convexo A, colocado atrás da lâmpada, tem por finalidade aumentar a intensidade da luz que incide no objeto (filme).
(B) o filamento da lâmpada deve situar-se no plano focal do espelho A, para que sua imagem real se forme nesse mesmo plano.
(C) a imagem projetada na tela é virtual, invertida e maior.
(D) a lente delgada C é convergente de borda delgada, possuindo índice de refração menor que o meio.
(E) as lentes plano-convexas B poderiam ser substituídas por lentes de Fresnel, menos espessas, mais leves, proporcionando menor perda da energia luminosa.
RESPOSTA: E
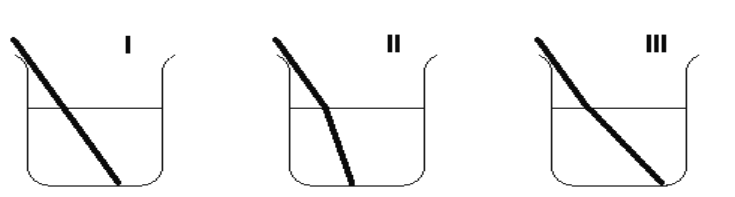
29$^a$ QUESTÃO
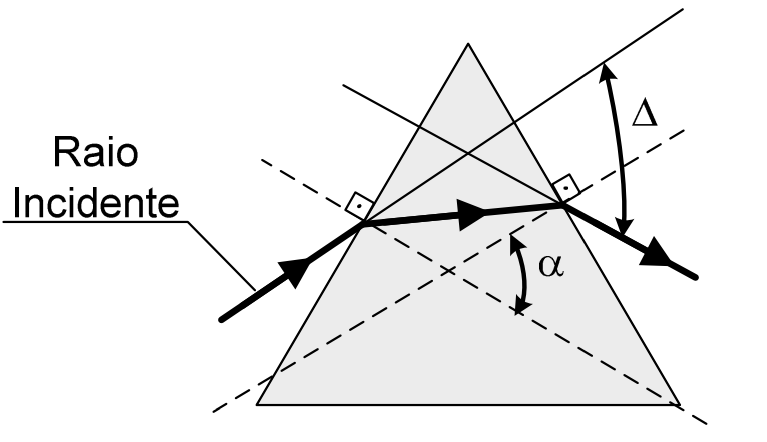
Um raio luminoso atravessa um prisma de vidro de índice de refração n, imerso em água, com índice de refração $n_{água}$. Sabendo que tanto o ângulo $\alpha$ como o ângulo de incidência são pequenos, a razão entre o desvio angular $\Delta$ e o $\alpha$ será
(A) $\frac{n}{n_{água}}-1$
(B) $\frac{n}{n_{água}}+1$
(C) $\frac{n}{n_{água}}-\frac 1 2$
(D) $\frac{n}{n_{água}}+\frac 1 2$
(E) $\frac{n_{água}}{n}-1$
RESPOSTA: A
RESOLUÇÃO

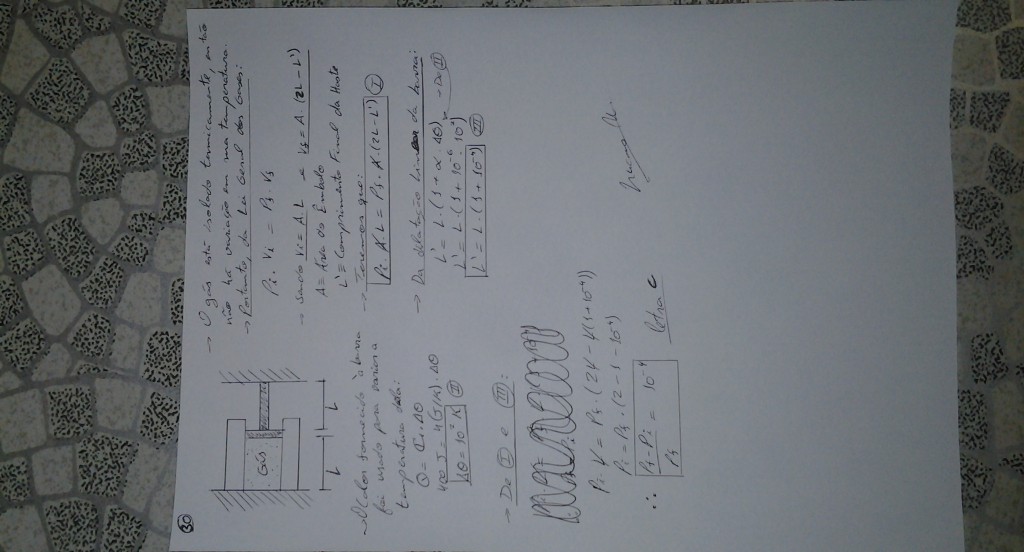
30$^a$ QUESTÃO
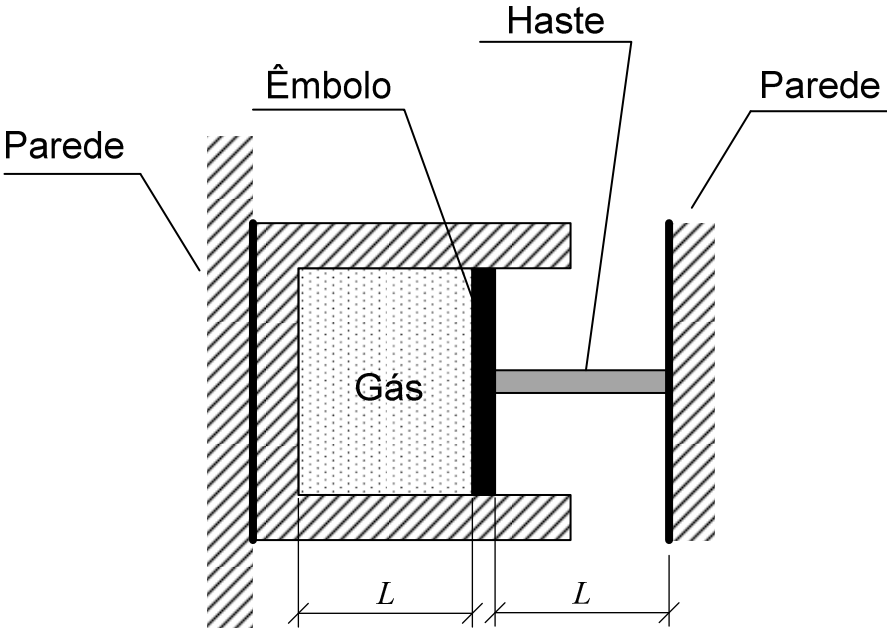
Um êmbolo está conectado a uma haste, a qual está fixada a uma parede. A haste é aquecida, recebendo uma energia de 400 J. A haste se dilata, movimentando o êmbolo que comprime um gás ideal, confinado no reservatório, representado na figura. O gás é comprimido isotermicamente.
Diante do exposto, o valor da expressão: $\frac{P_f-P_i}{P_f}$ é
Dados:
- pressão final do gás: $P_f$ ;
- pressão inicial do gás: $P_i$ ;
- capacidade térmica da haste: 4 J/K;
- coeficiente de dilatação térmica linear da haste: 0,000001 K$^{-1}$ .
(A) 0,01
(B) 0,001
(C) 0,0001
(D) 0,00001
(E) 0,000001
RESPOSTA: C
RESOLUÇÃO