O princípio de Pascal diz que a se produzirmos uma variação da pressão de um fluido em uma região qualquer do fluido, esta variação de pressão é integralmente transferida para todo o fluído, inclusive para toda a parede que contém o fluido.
Como principal aplicação direta deste princípio temos as prensas hidráulicas.
Observe a figura abaixo (extraída de https://pt.wikipedia.org/wiki/Prensa_hidr%C3%A1ulica)
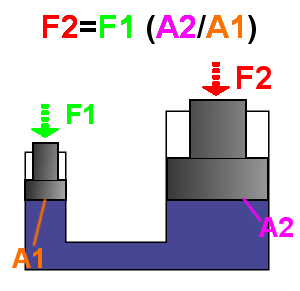
A pressão produzida pela força $F_1$ do lado esquerdo deve ser igual à do lado direito $F_2$ para que o sistema permaneça em equilíbrio estático. Assim, a pressão do lado esquerdo será $$p_1 = \frac{F_1}{A_1}$$ Enquanto que a pressão do lado direito será: $$p_2 = \frac{F_2}{A_2}$$ Como estas pressões são iguais, temos: $$p_1 = p_2 \Rightarrow \frac{F_1}{A_1}=\frac{F_2}{A_2}$$
EXEMPLO:
(ENEM 2013) Para oferecer acessibilidade aos portadores de dificuldades de locomoção, é utilizado, em ônibus e automóveis, o elevador hidráulico. Nesse dispositivo é usada uma bomba elétrica, para forçar um fluido a passar de uma tubulação estreita para outra mais larga, e dessa forma acionar um pistão que movimenta a plataforma. Considere um elevador hidráulico cuja área da cabeça do pistão seja cinco vezes maior do que a área da tubulação que sai da bomba. Desprezando o atrito e considerando uma aceleração gravitacional de 10 m/s2, deseja-se elevar uma pessoa de 65 kg em uma cadeira de rodas de 15 kg sobre a plataforma de 20 kg.
Qual deve ser a força exercida pelo motor da bomba sobre o fluido, para que o cadeirante seja elevado com velocidade constante?
a) 20 N
- b) 100 N
- c) 200 N
- d) 1000 N
- e) 5000 N
Usando o princípio de pascal: $$ \frac{F_1}{A_1}=\frac{F_2}{A_2} \Rightarrow \frac{F_1}{A_1}=\frac{F_2}{A_2}$$ Como a força aplicada em um dos lados do elevador é o peso da plataforma, mais o peso da cadeira de rodas e mais o peso da pessoa, temos: $$\frac{(20+15+65)\cdot g}{5 \cdot A_2}=\frac{F_{motor}}{A_2}$$ Lembrando que peso $P = m \cdot g $ e portanto $$ F_{motor}=\frac{100 \cdot 10}{5} =200 \rm{N}$$
