- Se uma fonte de ondas mecânicas viaja a uma velocidade superior às ondas produzidas, o conjunto de ondas produzidas permanecerão sempre dentro de um cone (caso tridimensional).
- Este cone é chamado de cone de Mach.
- A figura a seguir representa tal ideia.
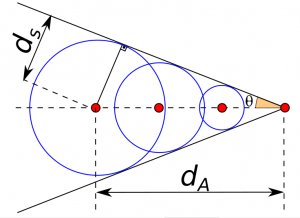
Cone de Mach representando o ângulo de Mach θ e as distâncias percorridas pelo avião e pelo som.
dS: distância percorrida pela onda (som, por exemplo)
dA: distância percorrida pela fonte (avião, por exemplo)
θ: ângulo de Mach
- Por geometria, temos:
$$\sin \theta=\frac{d_s}{d_A}$$
- Note que se o ângulo for medido e a velocidade da onda conhecida (esta hipótese é bem razoável) então podemos determinar a velocidade do avião:
$$d_A = {{d_S } \over {{\mathop{\rm sen}\nolimits} \theta }}\mathop \Rightarrow \limits^{ \div \Delta t} {{d_A } \over {\Delta t}} = {{{{d_S } \over {\Delta t}}} \over {{\mathop{\rm sen}\nolimits} \theta }} \Rightarrow $$
$$v_A = {{v_S } \over {{\mathop{\rm sen}\nolimits} \theta }}$$
- Unidade mach:
- É comum ouvir em filmes que a velocidade de um avião supersônico é mach 1, por exemplo. Esta medida expressa de quantas velocidade do som corresponde à velocidade do avião. Por exemplo, mach n significa que a velocidade do avião é
$$v_{A} = n \times v_{S} $$
- Note como o ângulo se relaciona com a unidade mach:
$$v_A = {{v_S } \over {{\mathop{\rm sen}\nolimits} \theta }} \Rightarrow n \cdot v_S = {{v_S } \over {{\mathop{\rm sen}\nolimits} \theta }} \Rightarrow $$
$$n = {1 \over {{\mathop{\rm sen}\nolimits} \theta }} \Leftrightarrow {\mathop{\rm sen}\nolimits} \theta = {1 \over n}$$
Observe a simulação a seguir. Acesse o link ao lado para interagir: https://www.desmos.com/calculator/9qaa4pa6fp