Se quiser um resumo, vá para o final do post. Além disso, estou assumindo algum conhecimento de física e matemática, mas não de cálculo (ensino superior). Tentei dar explicações simples de conceitos mais elaborados, entretanto alguns passos achei difíceis de explicar, portanto certamente teremos alguma perda de rigor.
Você já deve ter ouvido falar dessa tal de regra do tombo, certo? Se não, vou apresentá-la, sem entrar em detalhes. Ela será útil para lembrar de algumas fórmulas sem lançar mão daquelas “frases” tão usadas.
Primeiro, a “regra do tombo” exige que você tenha algum conhecimento prévio do assunto no qual você irá aplicá-la. Por exemplo, digamos que você sabe de antemão algumas fórmulas (sempre na forma de razão). Por exemplo, sabemos que \(v=\frac{\Delta S}{\Delta t}, \)\(a=\frac{\Delta v}{\Delta t}\)\( e F=\frac{\tau}{\Delta S}\).
Sendo \(v\) a velocidade, \(S\) o deslocamento, \(t\) o tempo, \(a\) a aceleração, \(\tau\) o trabalho, \(F\) a força e \(\Delta\) representa a variação de uma grandeza (isto é, a grandeza final menos a inicial).
Estes são apenas alguns exemplos, mas poderíamos usar muitos outros. Vamos então começar a falar o que é essa “regra”.
A grandeza do numerador (parte de cima da fração) deve depender da grandeza do denominador (parte de baixo da fração) e quem irá sofrer o tombo é a grandeza no denominador. Por exemplo, para achar a velocidade, temos de antemão que a posição deve depender do tempo e quem sofre o tombo é o tempo, pois este estaria no denominador. Vamos à um exemplo: sabemos que \(v=\frac{\Delta S}{\Delta t}\) para o caso em que a velocidade é constante, então comecemos com a equação da posição. Digamos que um corpo percorre uma trajetória retilínea tal que a equação horária é dada pela seguinte equação: \(s(t)=3t^2\)A “regra do tombo” diz para “derrubar” o expoente 2 do tempo (note que o tempo é quem está no denominador da equação que temos inicialmente). Esse expoente vai passar multiplicando o número 3, depois subtraímos um do expoente. Assim temos:
\(v=\rm{TOMBO}s_{em \; t} =2\cdot 3 t^{2-1}=6t\)
E esta é a equação da velocidade. Vamos para mais um exemplo?
Observe que a fração inicial, no caso anterior \(v=\frac{\Delta s}{\Delta t}\), só serve para sabermos a função (numerador, parte de cima da fração) que vamos tombar e o denominador (o que está em baixo da fração) nos diz quem vai sofrer o tombo (lembre-se de que esta equação é válida somente no movimento uniforme, mas ela nos auxilia a determinar qual função e qual variável irá “tombar”). Assim, mais um exemplo para a velocidade.
Seja dada a equação da posição \(s(t)=3t+2t^2\)Aplicando o tombo, temos:
\(v=\rm{TOMBO}s_{em \; t} =1\cdot 3 t^{1-1}+2\cdot 2t^{2-1}=3t^0+4t=3+4t\)
Como todo número elevado à zero é 1, então dizemos que \(t^0=1\) (na verdade isso é um pouco impreciso, pois \(0^0\) é uma indeterminação, assim por hora tomaremos \(t^0=1\) para todo o caso porque simplifica a nossa vida).
Ta muito fácil, não está? Vamos complicar um pouco… Seja a equação horária \(s(t)=3t^{\frac{4}{3}}+2\sqrt{t}\). Determine a equação da velocidade e da aceleração do móvel que obedece esta equação.
Vamos aplicar o tombo:
\(v=\rm{TOMBO}s_{em \; t} =\frac{4}{3} \cdot 3 t^{\frac{4}{3}-1}+\frac{1}{2}\cdot 2t^{\frac{1}{2}-1}\)
Observe que substituímos \(\sqrt{t}=t^{\frac{1}{2}}\)e aplicamos a “regra” normalmente. Continuando:
\(v=3t^{\frac{4}{3}-\frac{3}{3}}+t^{\frac{1}{2}-\frac{2}{2}}=4t^{\frac{1}{3}}+t^{\frac{-1}{2}} \Rightarrow \)
\(v=3\sqrt[3]{t}+\frac{1}{\sqrt{t}}\).
Ufa! Acabou…
Entendeu? Este processo é geral, ou seja, é aplicado para qualquer função \(f(x)\) desde que saibamos o que é a razão \(\frac{\Delta f(x)}{\Delta x}\). Quando constante, esta razão terá um significado, assim quando variável obtemos este significado pela regra do tombo. Abaixo vou dar mais alguns exemplos. Mas vamos para exemplos não numéricos, isto é, vamos usar algumas fórmulas conhecidas para chegar em outras.
MOVIMENTO UNIFORMEMENTE VARIADO
Vamos começar com a equação do “sorvetão”: \(s(t)=s_0+v_0t+\frac{1}{2}at^2\). Como já vimos, “tombamos” \(t\)para acharmos \(v\). Primeiro, vamos reescrever \(s(t)\) de maneira mais conveniente:
\(s(t)=s_0\cdot t^0+v_0 \cdot t^1+\frac{1}{2}a\cdot t^2\)
Aplicando o tombo: \(v=0+v_0\cdot 1+2\cdot \frac{1}{2} a \cdot t^{2-1} \Rightarrow \)\(v(t)=v_0+at\)
Sabemos que \(a=\frac{\Delta v}{\Delta t}\)quando a aceleração é constante, então aplicando o tombo na equação acima obtemos a aceleração. Verifique você mesmo que obterá \(a=a\) como tinha que ser… 🙂
FORÇA ELÁSTICA
Temos que começar com alguma fração conhecida. No caso, sabemos que \(F=\frac{\tau}{\Delta s}\). Quando comprimimos uma mola de uma distância \(\Delta s=x\), realizamos um trabalho
\(\tau = -\Delta E_{potencial}\),
isto é, “damos” energia potencial para a mola. Assim, podemos escrever que:
\(F_{elástica}=-\frac{\Delta E_{potencial}}{\Delta s}\)
Observe que esta equação seria válida somente para força constante, como a força peso, por exemplo, mas não para a mola que tem uma força variável. Se a força fosse constante a encontraríamos pela razão obtida, mas como não é temos que usar a regra do tombo. Assim, se soubermos a energia potencial de uma mola conseguimos descobrir a força.
Com isso, sabendo que \(E_{potencial}=\frac{kx^2}{2}\)aplicamos o tombo em \(x\):
\(F_{elástica}=-2\cdot \frac{k\cdot x^{2-1} }{2} \Rightarrow \)\(F_{elástica}=-kx\).
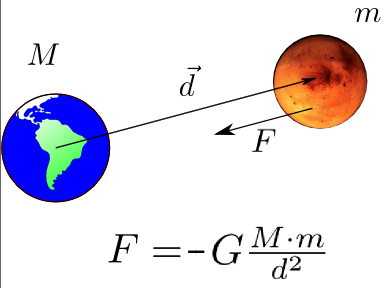
FORÇA GRAVITACIONAL
Para finalizar, lembremos da fórmula da energia potencial gravitacional:
\(E_{pot}=-\frac{GMm}{d}=-GMmd^{-1}\).
Por uma discussão análoga à anterior, aplicando o “tombo” em \(d\) obtemos a força gravitacional:
\(F_{grav}=-\left [-(-1)GMmd^{-1-1}\right ]\Rightarrow \)\(F_{grav}=-\frac{GMm}{d^2}\).
Os sinais aqui confundem um pouco, mas o que importa é que chegamos na forma da força gravitacional. O sinal de menos é interpretado da seguinte forma: a força gravitacional é oposta ao vetor posição.
A sugestão que deixo é que não se preocupe com o sinal, pois a explicação mais detalhada do sinal vem de um assunto que é abordado no ensino superior chamado de gradiente.
Você pode fazer isso para a energia potencial gravitacional próxima à superfície da Terra:
\(E_{pot}=mgh\Rightarrow F_{grav}=-mg\).
O sinal de menos surge porque a força é para baixo, sendo a altura medida de baixo para cima.
FORÇA ELÉTRICA
Esta fica como exercício…
Sabendo a energia elétrica:
\(E_{pot}=K\frac{Q\cdot q}{d}\),
você deverá obter parfa o módulo da força a seguinte relação:
\(F=K\frac{Q\cdot q}{d^2}\).
Na realidade, tomando um referencial simular ao discutido para força gravitacional, podemos dizer que esta relação também leva em conta os sinais das cargas. Reflita sobre isso: se as cargas tiverem o mesmo sinal, a força é repulsiva, afinal obteremos um valor negativo para ela; se as cargas tiverem sinais opostos, a força elétrica é atrativa, afinal obteríamos a força com um valor negativo.
M.H.S.
Acredito que este seja o ponto mais útil da “regra do tombo”, pois demonstrar todas as equações do M.H.S. sem usar esta ferramenta é mais trabalhoso.
Primeiro temos que aprender como aplicar a regra do tombo para funções trigonométricas, pois a equação do M.H.S. é \(x(t)=Acos(\omega t +\phi _0)\). Abaixo, temos a esquerda uma função trigonométrica e à direita a mesma função “tombada”:
\(\rm{sen} x \Rightarrow \rm{cos} x\)
\(\rm{cos} x \Rightarrow -\rm{sen} x\)
Usaremos isso logo abaixo. Mas antes temos que entender a regra do tombo para funções compostas (ou regra da cadeia).
Seja uma função composta \(f(g(x))\). Para aplicar a regra do tombo, nós consideramos que \(g(x)=y\), sendo \(y\) outra variável, “tombamos” \(f(y)\) em relação à \(y\) e multiplicamos o resultado por \(g(x)\) “tombada”.
Vamos à um exemplo.
Seja \(f(x)=5 \cdot \rm{sen}(2x^3+8)\). Para tombar \(f(x)\) temos que perceber que esta é uma função composta em que \(f(x)=f(g(x))\) e \(g(x)=2x^3+8\). Pelo procedimento descrito acima, escrevemos \(g(x)=y\) e tombamos \(f(y)\) em relação à \(y\):
$$f(y)=5\rm{sen}y \Rightarrow 5\rm{cos}y.$$
Depois tombamos \(g(x)=y\) e multiplicamos pelo resultado anterior: $$g(x)=2x^3+8 \Rightarrow 6x^2$$.
Multiplicando os dois temos: $$5\cdot \rm{cos}(2x^3+8)\cdot 6x^2=30x^2\cdot\rm{cos}(2x^3+8).$$
Agora vamos tentar com a equação do M.H.S.. Temos primeiro a equação da posição: \(x(t)=Acos(\omega t +\phi _0)\). Lembrando que tombar \(x\) em relação ao tempo encontra-se a velocidade, então: $$v(t) = A\cdot -sen(\omega t +\phi _0) \cdot(\omega) \Rightarrow $$
$$v(t)=-A \omega \rm{sen}(\omega t + \phi _0).$$
O termo que coloquei entre parêntesis na frente da primeira igualdade é o “tombo” aplicado no termo de dentro da função trigonométrica.
Se aplicarmos a regra novamente encontramos a aceleração: $$a(t)=-A\omega ^2 \rm{cos}(\omega t + \phi _0).$$
Observe que \(a = -\omega ^2 x\) e esta é uma equação extremamente importante no M.H.S..
RESUMÃO
Regra do tombo para polinômios:
$$x^n \overset{\rm{tombo}}{\Rightarrow} n\cdot x^{n-1}$$
Regra do tombo para funções trigonométricas:
$$\rm{sen} x \overset{\rm{tombo}}{\Rightarrow} \rm{cos} x$$
$$\rm{cos} x \overset{\rm{tombo}}{\Rightarrow} -\rm{sen} x$$
Funções compostas:
$$f(g(x))=f(y)\overset{\rm{tombo}}{\Rightarrow} (\rm{tomba} \; f(y))\cdot (\rm{tomba}\; g(x))$$