O seguinte comentário foi postado em Pergunte ao Professor Danilo por Dirlei santos:
58 – Um estudante montou um experimento com uma rede de difração de 1000 linhas por milímetro, um laser que emite um feixe cilíndrico de luz monocromática de comprimento de onda igual a m 4.10−7 e um anteparo, conforme figura abaixo.
O espectro de difração, observado no anteparo pelo estudante, foi registrado por uma câmera digital e os picos de intensidade apareceram como pequenos pontos
brilhantes na imagem.
Nessas condições, a opção que melhor representa a imagem do espectro de difração obtida pelo estudante é:
a) . . .
b) . . . .
c) . . . . .
d) . . . . . . .
Não entendi essa questão, teria como me explicar ? Fica a vontade que eu gosto de física, vou tentar entender ao máximo.
Demorei um pouco para responder porque não queria colocar a resolução apenas com a fórmula: pensei em explicar o que está acontecendo.
Primeiramente, vamos ao que é rede de difração: imagine uma placa com vários cortes ao longo delas, todos paralelos entre si. Os cortes têm largura pouco maior que o comprimento de onda da onda incidente. Um exemplo disso é o cd (ou dvd e o blu-ray). Veja a foto abaixo com um experimento feito em casa com laser verde e um cd sem a parte prateada.
Acima, um pedaço de CD sem a parte metálica. Abaixo o pedaço de CD fixo em um prendedor de papel.
Ao passar o laser por ele, o que acontece?
Os pontos que você vê é a imagem de difração da rede que existe no cd. Usei o laser verde de comprimento de onda de 532 nm, assim, além de resolver o exercício vamos calcular a distância entre duas linhas no cd. Abaixo, a distância da rede (cd) ao anteparo (parede).
Vamos ao exercício.
Se procurar a solução na internet vai ver que se usam a fórmula
$$d \; \rm{sen} \theta = m \lambda $$
Vamos demonstrar esta fórmula.
Primeiro, você deve saber um pouco sobre interferência de ondas. Lembra-se que duas ondas emitidas por duas fontes em fase (em fase quer dizer que quando uma onda produzida está “subindo”, a outra também está, e quando está “descendo”, a outra também está) quando as duas se encontram pode haver interferência construtiva e destrutiva?
Se a diferença entre as distâncias percorridas por ambas as ondas for um múltiplo inteiro do comprimento de onda \(\lambda\) então ocorrerá uma interferência construtiva. É importante você saber do que estou falando para entender o restante! Se não souber, pode perguntar.
Vamos lá: abaixo está representado o perfil da rede de difração que estamos estudando:
À esquerda está representado o laser e à direita os pontos de máximos (onde ocorre interferência construtiva). Cada fenda na rede se comporta como se fosse uma fonte emitindo uma onda em fase. Vamos dar um “zoom” na rede e analisar um raio de luz que sai de cada fenda:
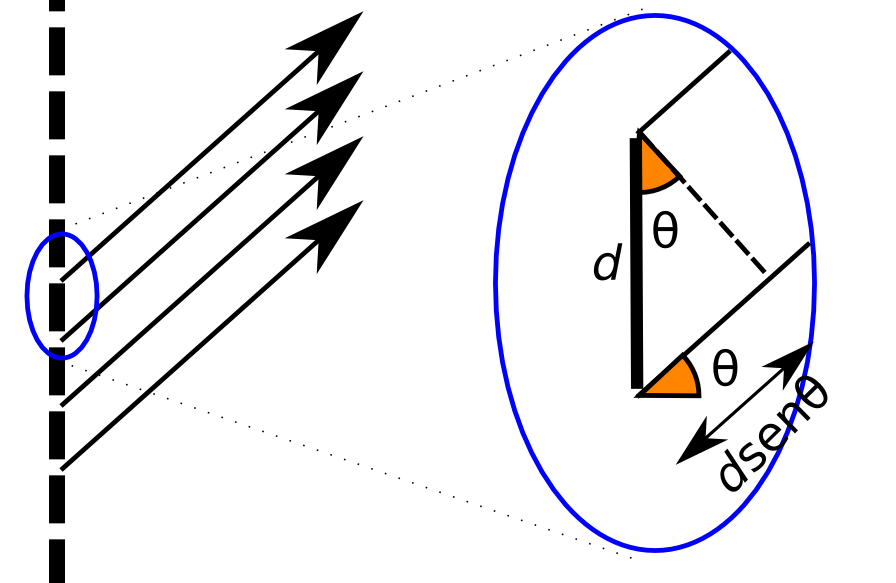
Na figura estão representados os raios que saem da rede e atingem o ponto onde ocorre o primeiro máximo de interferência, isto é, o primeiro ponto brilhante contado do centro para fora, mas desconsiderando o máximo central.
Como a distância entre as fendas d é muito pequena comparada com a distância entre a rede e o anteparo podemos considerar os raios que saem das fendas como paralelos. Na figura à direita está representado um trecho da rede onde está sendo mostrado a distância d entre duas fendas e a diferença de caminho entre dois raios consecutivos, que é dada por \(d\;\rm{sen} \theta\). Assim, temos a fórmula, pois a diferença de caminho deve ser um múltiplo inteiro (que chamaremos de \(m\)) de \(\lambda\):
diferença de caminho = número inteiro vezes comprimento de onda \(\Rightarrow\)
$$d \; \rm{sen} \theta = m \; \lambda.$$
Note que o enunciado nos deu a quantidade de linhas por milímetro, assim sabemos que a distância entre cada fenda é:
$$d=\frac{1\; \rm{mm}}{1000}=1\cdot 10^{-6}\;\rm m.$$
A pergunta é quantos máximos o estudante enxerga no anteparo. Para que apareça um ponto brilhante na parede, é necessário que \(\theta < 90^o\), pois se \(\theta > 90^o\) a luz foi refletida. Assim, para a condição de \(\theta = 90^o\) temos:
$$d \; \rm{sen} \theta = m \; \lambda \Rightarrow$$
$$1\cdot 10^{-6}\;\rm{sen}90^o=m\cdot 4\cdot 10^{-7}\Rightarrow$$
$$m=\frac{10}{4}\Rightarrow$$
$$m=2,5.$$
Como \(m\) deve ser inteiro, devemos arredonda-lo para menos, pois \(m = 3\) implica em \(\theta > 90^o\). Assim, temos que \(m = 2\).
Ou seja, estamos falando do segundo máximo, sem contar o central. Como a imagem é simétrica, temos mais dois pontos do outro lado, isto é, temos 5 pontos de máximos.
$$\rm{Resposta\;C}.$$
Voltando ao nosso exemplo, que montei com um CD, você deve ter reparado que apareceram apenas três pontos. Mesmo aproximando o CD da parede o número não aumenta.
Vamos tentar calcular o número de linhas por unidade de comprimento do CD?
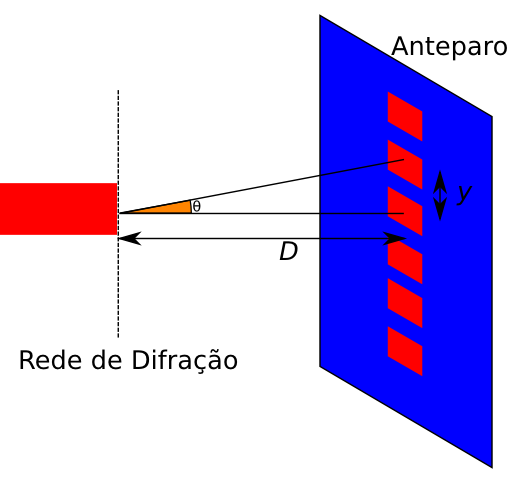
Por trigonometria, pelo desenho anterior, vemos que
$$\rm{tg}=\frac{y}{D}$$
Como em nosso experimento \(m = 1\), \(y=7\;\rm{cm}\) e \(D=17\;\rm{cm}\), podemos montar o seguinte sistema:
$$\left\{\begin{matrix}
d\;\rm{sen}\theta=m\;\lambda\\
\rm{tg}\theta=\frac{y}{D}
\end{matrix}\right.
\Rightarrow
\left\{\begin{matrix}
d\;\rm{sen}\theta=1\cdot532\cdot10^{-9}\\
\rm{tg}\theta=\frac{7}{17}
\end{matrix}\right.
\Rightarrow $$
$$\left\{\begin{matrix}
d\;\rm{sen}\theta=532\cdot10^{-9}\\
\theta=22,38^o
\end{matrix}\right.$$
O ângulo eu descobri usando uma calculadora científica. Assim, substituindo o resultado da equação de baixo na equação de cima e usando uma calculadora científica, temos:
$$d\;\rm{sen}22,38^o=532\cdot10^{-9}\Rightarrow d\cdot0,381=532\cdot10^{-9}\Rightarrow $$
$$d=1,397\cdot10^{-6}\;\rm m$$
Ou seja, quase 1,4 \(mu\;\text{m}\) entre uma ranhura e outra.
O número de ranhuras por milímetro é \(\frac{1}{d}\) sendo d em milímetro, ou seja:
$$\frac{1}{1,4\cdot 10^{-3} \;\rm{mm}}=714 \; \rm{ranhuras}\;\rm{por}\;\rm{mm}$$
Segundo a literatura, o valor é de 625 ranhuras por mm. Não está tão longe assim para um experimento tão simples, feito com régua, em casa.
Vamos voltar ao desenho anterior.
Muitas vezes a seguinte aproximação pode ser feita:
$$\rm{sen}\theta\approx\rm{tg}=\frac{y}{D}$$
Se assim for, podemos reescrever o sistema anterior tornando-o mais simples:
$$\left\{\begin{matrix}
d\;\rm{sen}\theta=m\;\lambda\\
\rm{sen}\theta\approx\frac{y}{D}
\end{matrix}\right.
\Rightarrow$$
$$d=\frac{m\;\lambda\;D}{y}$$
