Hoje veremos como programar um semáforo em Arduíno. A impressão foi feita por mim para ser usada nas aulas, no entanto vou compartilhar o desenho e o processo de como fiz a montagem.
O Semáforo 3D
O desenho foi feito no Tinkercad e pode ser visualisado a seguir.
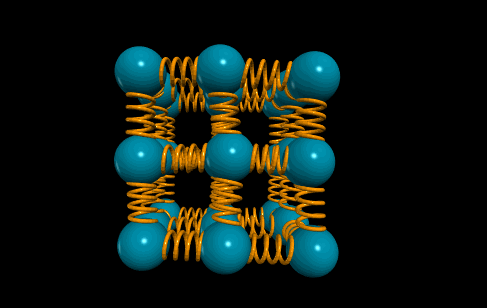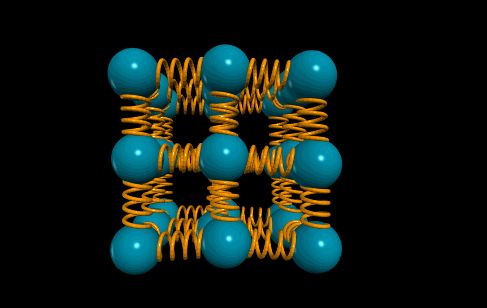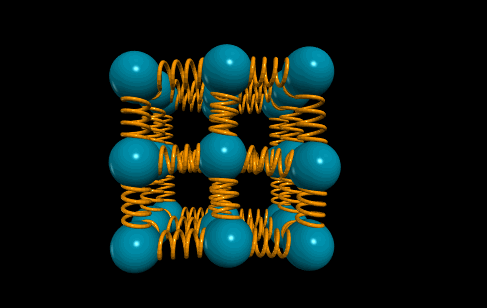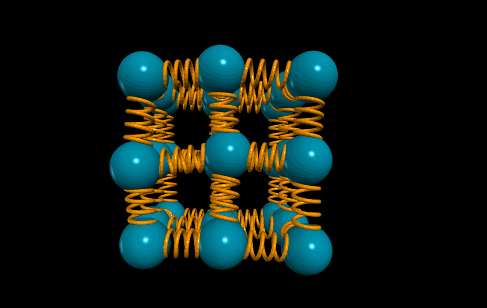
Os LEDs foram colados com cola escolar líquida (de PVC) usada pra colar papel e outros materiais escolares. O resultado final ficou como nas fotos a seguir.

Para conectar os LEDs aos fios que vão ao Arduino, tentei duas estratégias: soldar fios aos LEDs e conectar diretamente um fio M/F aos LEDs. A segunda opção se saiu melhor.


Apesar de decidir por não soldar os cabos os fios nos LEDs, achei bom colar os GNDs dos LEDs um no outro, diminuindo o uso de fios por parte dos alunos.

O circuito no Tinkercad
Confira o circuito abaixo:
Se o circuito não carregar, acesse o circuito na página do Tinkercad.
O código
Baixe, compartilhe ou copie o código acessando o site do GitHub.
Vamos discutir o código a seguir.
Primeiramente inserimos variáveis com valores que correspondem às portas digitais a serem usadas.
int verde1 = 2, amarelo1 = 3, vermelho1 = 4, verde2 = 5, amarelo2 = 6, vermelho2 = 7;
No setup, configuramos cada uma das portas acima como saída.
void setup() {
pinMode(verde1, OUTPUT);
pinMode(amarelo1, OUTPUT);
pinMode(vermelho1, OUTPUT);
pinMode(verde2, OUTPUT);
pinMode(amarelo2, OUTPUT);
pinMode(vermelho2, OUTPUT);
}
No loop, vamos detalhar um pouco mais. Começando com a parte do código que liga o LED verde do semáforo 1 e o vermelho do semáforo 2 e aguarda 2 segundos (2000 milissegundos).
void loop() {
digitalWrite(verde1, HIGH);
digitalWrite(vermelho2, HIGH);
delay(2000);
Para mudar o semáforo 1 para amarelo precisamos desligar o verde e só então ligarmos o verde. Fazemos isso e aguardamos mais um segundo:
digitalWrite(verde1, LOW); digitalWrite(amarelo1, HIGH); delay(1000);
Para mudar o semáforo 1 para vermelho temos que desligar o LED amarelo do semáforo 1. Logo em seguida, para mudar o semáforo 2 para verde, temos que desligar o LED vermelho do semáforo 2 e ligar o LED verde do semáforo 2. Depois, aguardamos mais 2 segundos.
digitalWrite(amarelo1, LOW); digitalWrite(vermelho1, HIGH); digitalWrite(vermelho2, LOW); digitalWrite(verde2, HIGH); delay(2000);
Para colocar o semáforo 2 no amarelo precisamos desligar o LED verde e ligar o amarelo. Aguardamos mais um segundo no final:
digitalWrite(verde2, LOW); digitalWrite(amarelo2, HIGH); delay(1000);
Por fim, deligamos o amarelo do semáforo 2 e o vermelho do semáforo 1.
digitalWrite(amarelo2, LOW); digitalWrite(vermelho1, LOW); }
Note que ao terminar o algoritmo o Arduino volta a executar tudo desde o começo, portanto, não precisamos escrever mais nada. Para verificar, veja abaixo o início do nosso código novamente:
digitalWrite(verde1, HIGH); digitalWrite(vermelho2, HIGH);
Resultado final do projeto
Confira no vídeo a seguir o resultado final. Minha câmera não é boa, portanto o vídeo vai começar já na parte em que mostro o circuito funcionando. Em seguida discuto o código. A montagem do circuito ficou prejudicada e não recomendo o vídeo desde o começo.