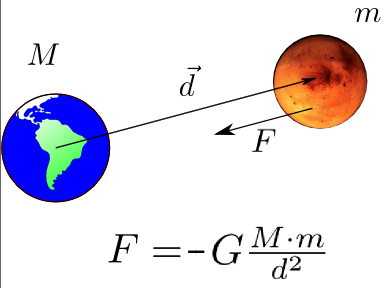
Um assunto recorrente no vestibular mas que muitos alunos têm muita dificuldade é a estática de corpo extenso. Isso porque há um conceito novo: o torque.
Com um exemplo prático vou tentar explicar como calcular o torque e como usar isso na resolução de um problema.
Para começar, vamos abordar alguns assuntos importantes que talvez você não conheça. São eles:
- Ponto de giro;
- Torque;
- Linha de ação;
- Braço.
O que é ponto de giro? Na verdade, é um ponto qualquer que você escolhe no seu problema. Vamos deixar assim, meio abstrato mesmo, depois veremos melhor o que é isso.
Torque é o produto da força pelo braço da força. Legal, mas o que é braço?
Braço é a distância entre o ponto de giro e a linha de ação da força. Tá ficando engraçado, pois o que é linha de ação de uma força?
Seja uma força qualquer: desenhe uma linha tracejada que passe por cima do vetor força. Esta linha é a linha de ação da força.
Vamos juntar alguns conceitos novos na lista abaixo, pois são conceitos importantes:
Vamos ver alguns destes conceitos, de forma mais abstrata, em um desenho.
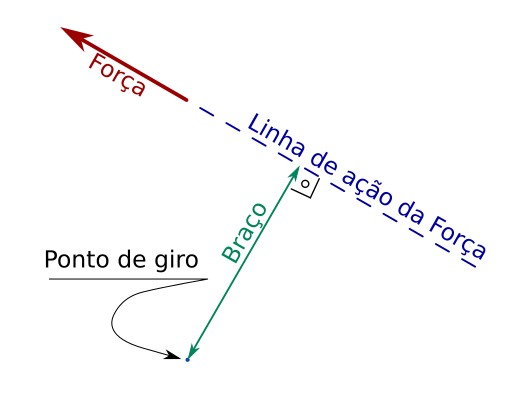
Como braço é uma distância, vamos chamá-lo de d, assim a definição de torque é:
\(T=F\cdot d\). \(\;\;\;\;\;\) EQUAÇÃO (1)
Vamos complicar um pouco mais, porém com o objetivo de explicar melhor os conceitos e no final simplificar (você vai ver que na maioria dos problemas, as coisas serão bem mais simples… só estou tentando explicar os conceitos corretamente).
Uma força alternativa de calcular o torque (você vai ver a formula a seguir em alguns livros) é:
T=F⋅r⋅senθ.
Aqui, usei r, que é a distância entre o ponto de giro e o local onde a força é aplicada. O ângulo θ é o ângulo entre o vetor posição \(\vec r\) (vetor com origem no ponto de giro e final onde a força é aplicada) e a força \(\vec F\). Vejamos em desenho:
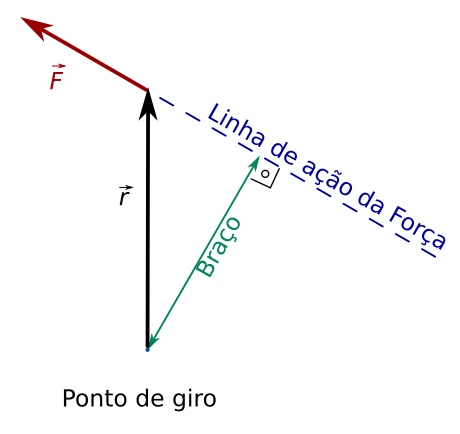
Lembre-se que o ângulo entre dois vetores é o menor ângulo entre eles quando ambos estão com uma origem em comum. Assim, vamos colocar os vetores força e posição com a mesma origem.
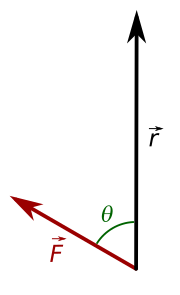
Voltemos à figura anterior e verifiquemos que r⋅senθ=d
, isto é, é o braço que eu havia definido lá no começo.
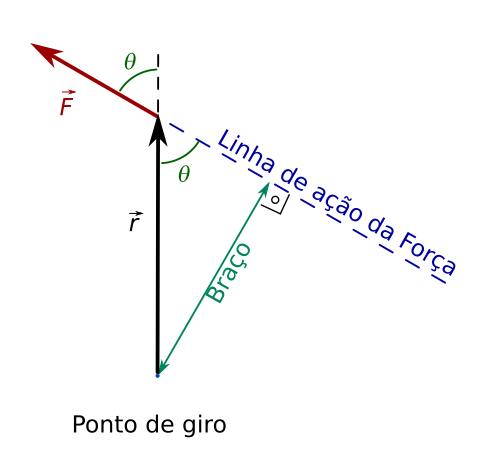
Da figura acima, vemos que
$$sen\theta=\frac{cateto\;oposto}{hipotenusa}\Rightarrow$$senθ=dr⇒
d=r⋅senθ.
Para um sistema ficar em repouso, além da soma das forças ser zero, é necessário que a soma dos torque sejam nulas. Por exemplo, digamos um corpo extenso sobre o qual agem duas forças: o peso e mais uma força que você faça. Por exemplo, uma caneta. Mesmo se a força que você fizer nela for igual ao peso, dependendo de onde você aplica, a caneta não fica em repouso. Na figura abaixo, temos uma caneta com a força peso representada no seu centro de massa:
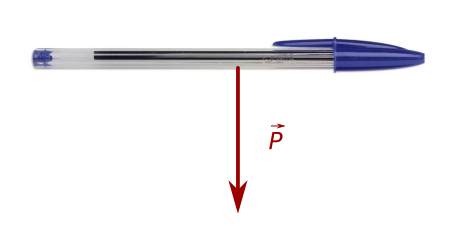
Digamos que você faça uma força sobre ela idêntica ao peso, mas para cima. Com certexa, o centro de gravidade da caneta não irá mudar a altura, mas a caneta irá girar. Veja isso no desenho abaixo:

Intuitivamente, percebemos que a caneta gira no sentido horário (em relação ao ponto onde está aplicada a força peso que pode ser o ponto de giro escolhido para este problema). Veja que aqui teremos um torque. Vamos indicar a rotação da caneta e o torque que age nela.
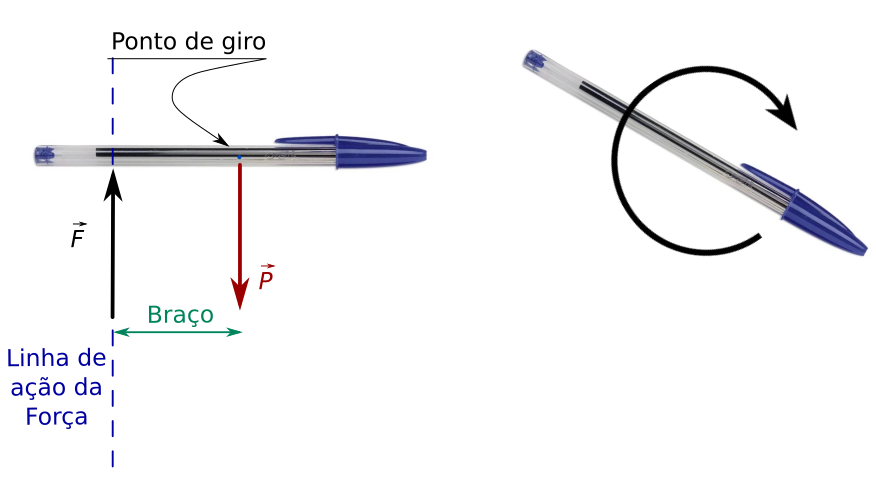
Olha como o braço fica fácil de ser identificado, veja também que se você imaginar o ponto de giro fixo, vemos o sistema girando no sentido horário em torno do ponto de giro. Outra coisa interessante é que se você escolher o ponto de giro como sendo onde está aplicada a sua firça, não tem proble, pois podemos imaginar que a caneta gira em torno do ponto que você escolheu. Veja isso na figura abaixo e perceba que a conclusão é a mesma: a caneta gira no sentido horário.
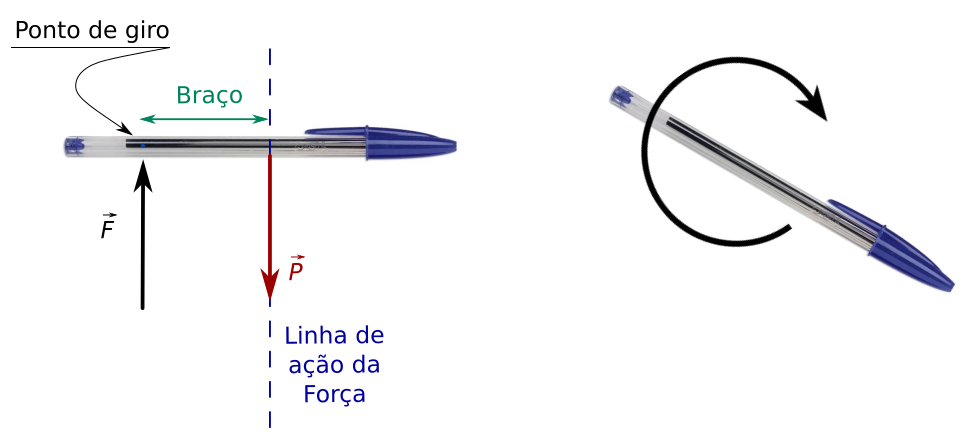
Nesta situação, o torque no sentido horário é:
T=F⋅(Braço)
ou, que da a mesma coisa:
T=F⋅P.
Mas o que nos interessa é que o sistema não gire, então vamos colocar mais uma força nesta caneta para que ela não rotacione. Logicamente, a soma das duas forças que você irá fazer deve ser igual ao peso da caneta, então vamos impor isso:
F1+F2=P
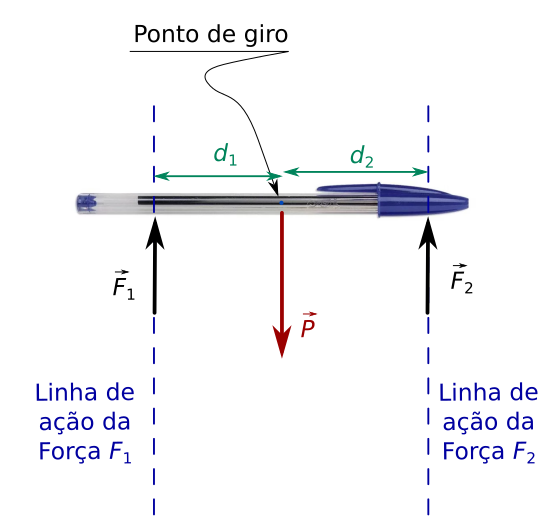
Neste caso, o torque no sentido horário (\(T_{horario}=F_1\cdot d_1\)) deve ser igual ao torque no sentido anti-horário (\(T_{anti-horario}=F_2\cdot d_2\)). Assim, podemos escrever que:
\(T_{horario}=T_{anti-horario}\)
ou ainda que
\(F_1\cdot d_1=F_2\cdot d_2\)
Felizmente, a maioria dos problemas é fácil localizar os braços e forças.
Legal, mas se tivermos forças de 1 a 5 tentando girar no sentido horário e 6 à 10 no sentido anti-horário, como faríamos?
Somamos os torque no sentido horário e igualamos ao torque no sentido anti-horário.
\(F_1 \cdot d_1 + F_2 \cdot d_2 + F_3 \cdot d_3 + F_4 \cdot d_4 + F_5 \cdot d_5 =\)\(F_6 \cdot d_6 + F_7 \cdot d_7 + F_8 \cdot d_8 + F_9 \cdot d_9 + F_10 \cdot d_10\).
Podemos usar o simbolo de somatório para simplificar e generalizar.
Sejam m forças agindo no sentido horário e n forças no sentido anti-horário. Para que um corpo extenso fique em repouso (estático) é necessário que a soma dos torque no sentido horário seja igual à soma dos torque no sentido anti-horário, isto é:
\(\sum_{i=1}^{m}F_i \cdot d_i=\sum_{j=1}^{n}F_j \cdot d_j\). \(\;\;\;\;\;\;\;\;\;\;\)EQUAÇÃO (2)
Espero que isso ajude você que possui algumas dificuldades com este assunto.
Ah, mas será que respondi à todas as perguntas? Acho que não. Então vamos lá:
O que é?
A equação (1) responde a essa pergunta.
Como usar?
Você soma todos os torque em um sentido (por exemplo, horário) e iguala à soma dos torques no sentido oposto(por exemplo, anti-horário).
Quando usar?
Sempre que tivermos um exercício de física que trata de um corpo em repouso porém este corpo não pode ser considerado pontual. Ou seja, usamos quando o problema trata de estática de corpo extenso.
Em breve, pretendo fazer algumas resoluções de exercícios de estática e disponibilizar aqui para vocês. Quando fizer, colocarei neste mesmo post um adendo com os exercícios e caso eu demore para fazer isso, crio um novo post só para apontar para este daqui.