Arquivo mensais:outubro 2018

Ondas estacionárias

1 resposta

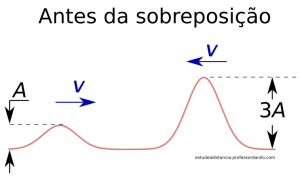
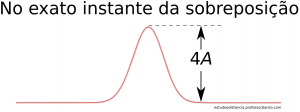
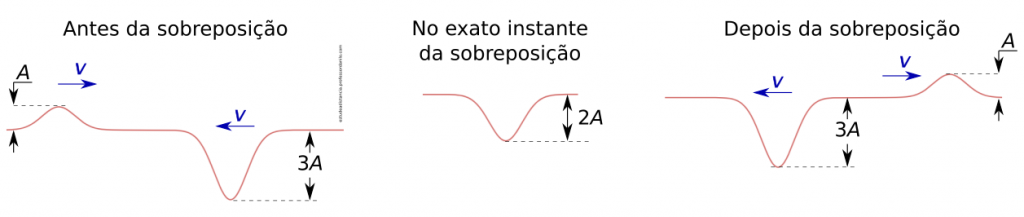
Algumas animações sobre ondas estacionárias… Todas elas podem ser acessadas no Desmos, simulações estas que podem ser modificadas deliberadamente. Seguem os links:

Tubo com duas extremidades fechadas: https://www.desmos.com/calculator/furozafpzb

Tubo com ambas as extremidades abertas: https://www.desmos.com/calculator/hhpc9jfdbl

Tubo com uma extremidade aberta e outra fechada: https://www.desmos.com/calculator/grdqitedta

Vamos imaginar uma corda de comprimento L e produzir uma onda nela: o resultado que vamos obter corresponde à uma onda parada, uma vez que a onda fica presa na corda e acaba interferindo-se com ela mesma.

Tal assunto também é abordado quando falamos de tubos sonoros, no entanto somente poderemos falar de tubos sonoros quando tivermos um tubo com uma extremidade aberta (chamado tubo fechado) ou com ambas abertas (chamado tubo aberto). Se ambas as extremidade forem fechadas, então NÃO temos um tubo sonoro.

ONDA ESTACIONÁRIA COM AMBAS AS EXTREMIDADES FIXAS

Seja o primeiro harmônico:

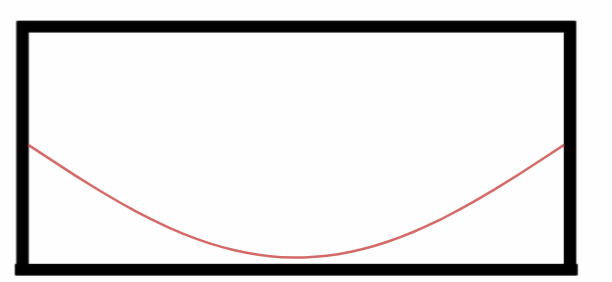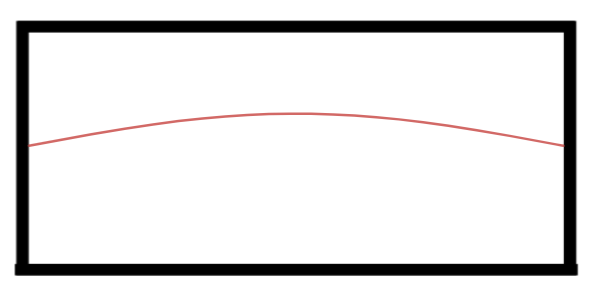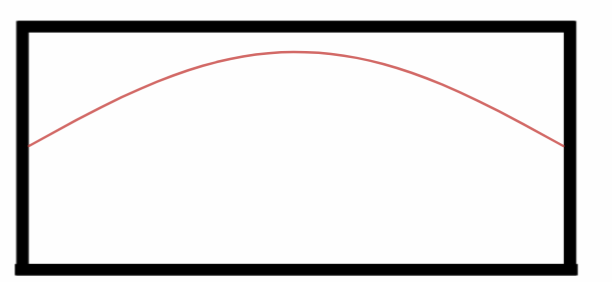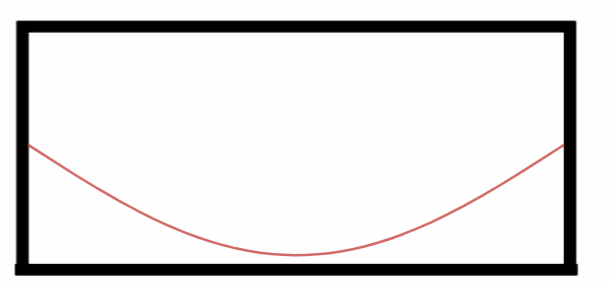
Primeiro Harmônico ou Harmônico fundamental.

Observe nós vemos apenas metade de uma onda, logo podemos dizer que o comprimento da onda aqui presenta é: $$L=\frac{\lambda_1}{2}\Rightarrow$$ $$\lambda_1 = 2\cdot L.$$

Vamos para o segundo harmônico:

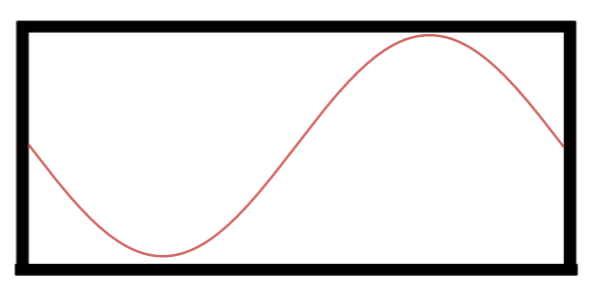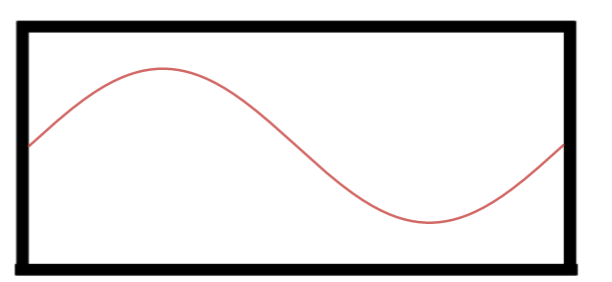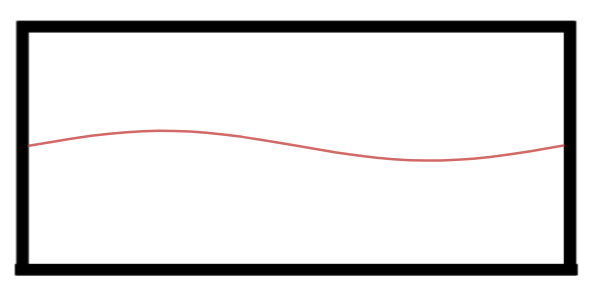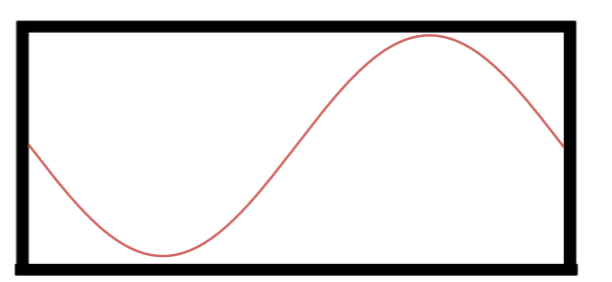
Segundo Harmônico.

Note que agora o há exatamente um comprimento de onda dentro do tubo, com isso temos $$L=\lambda_2\Rightarrow$$ $$\lambda_2=L$$

Observe que agora no terceiro harmônico temos mais meio comprimento de onda dentro do tubo:

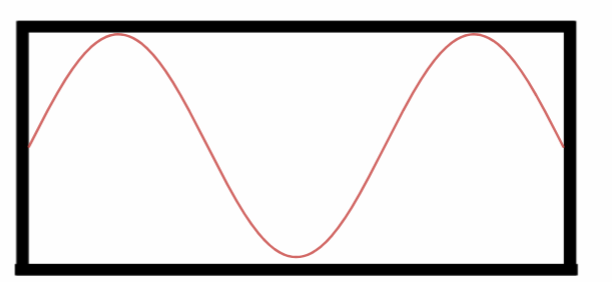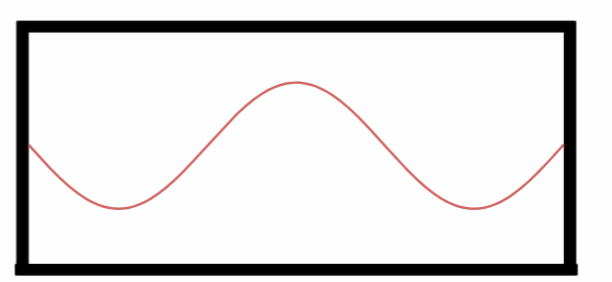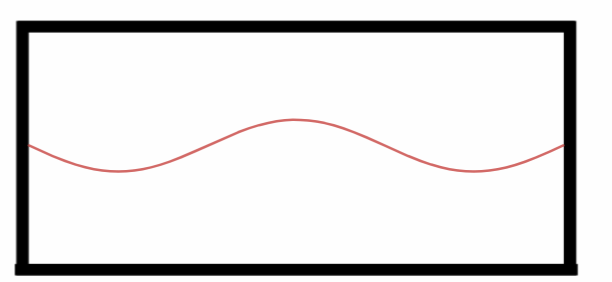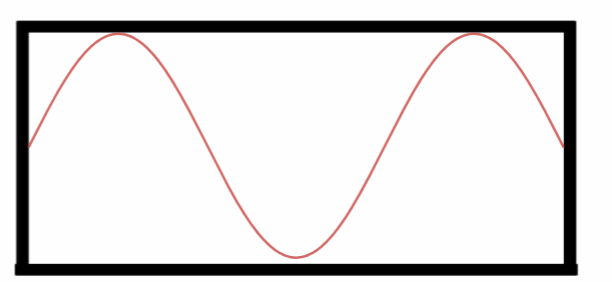
Terceiro Harmônico.

No terceiro harmônico temos: $$L=3\cdot \frac{\lambda_3}{2}\Rightarrow$$ $$\lambda_3=\frac{2L}{3}.$$

Se continuarmos com os demais estados estacionários vemos que o caso geral para o n-ésimo harmônico é $$\lambda_n=\frac{2L}{n}.$$

Vamos continuar com mais animações de estados estacionários.

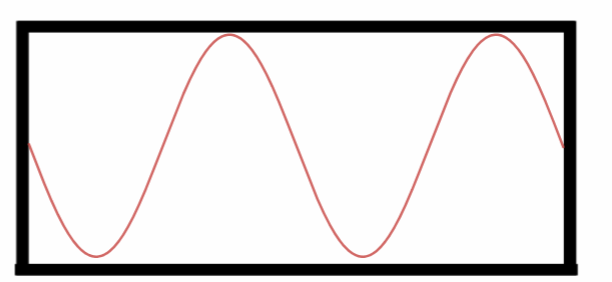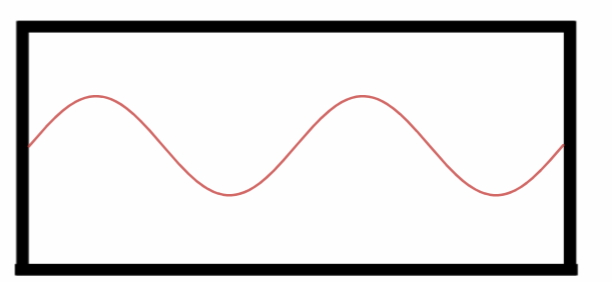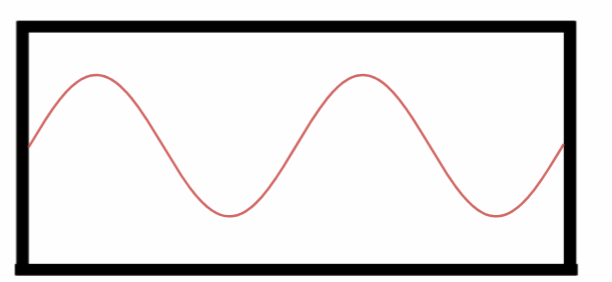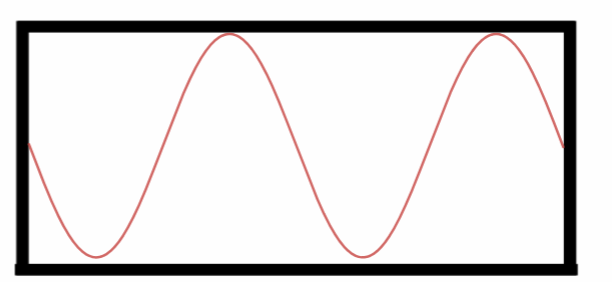
Quarto Harmônico.

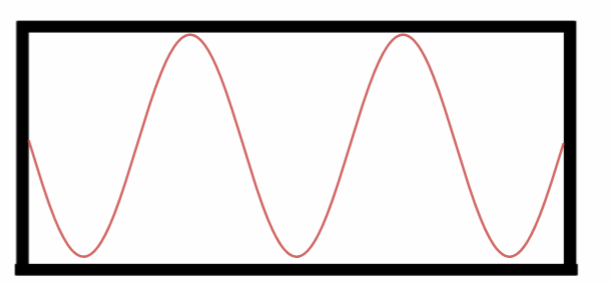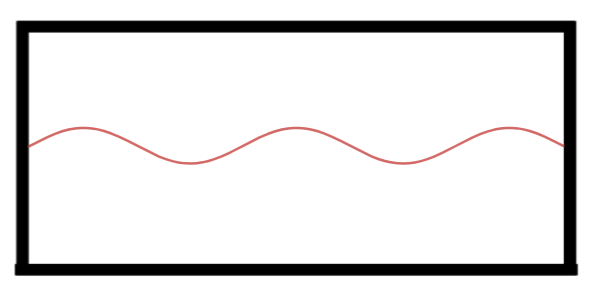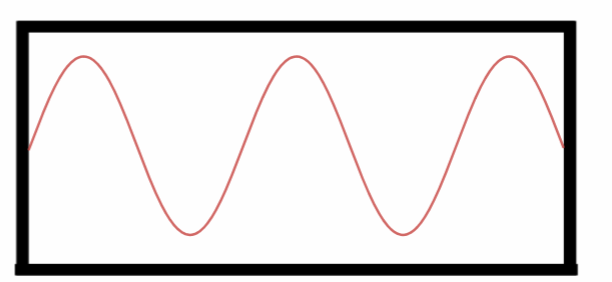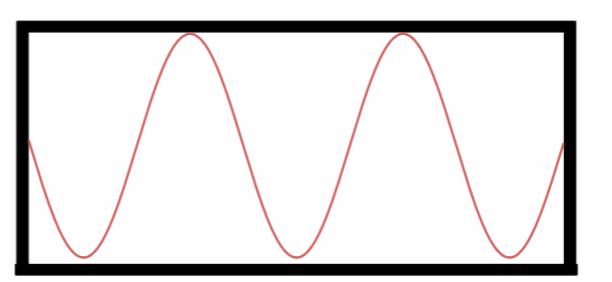
Quinto Harmônico.

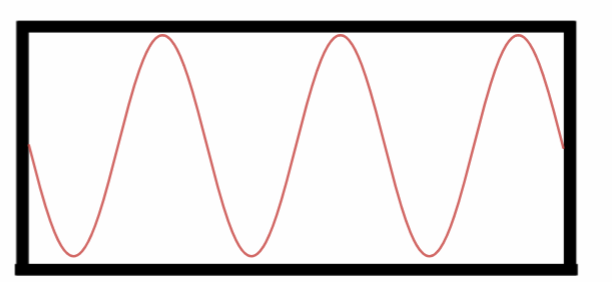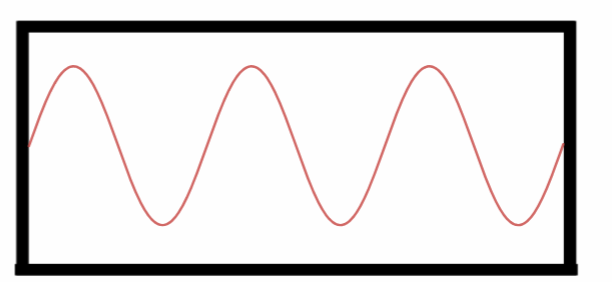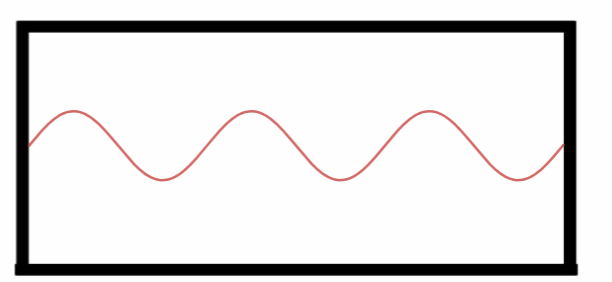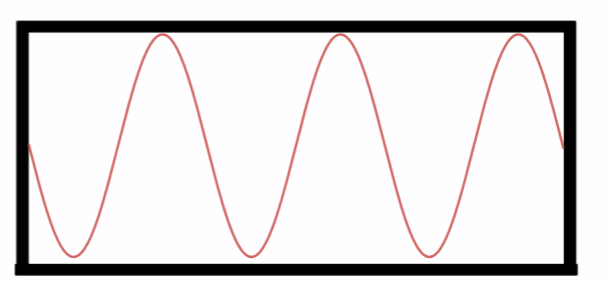
Sexto Harmônico

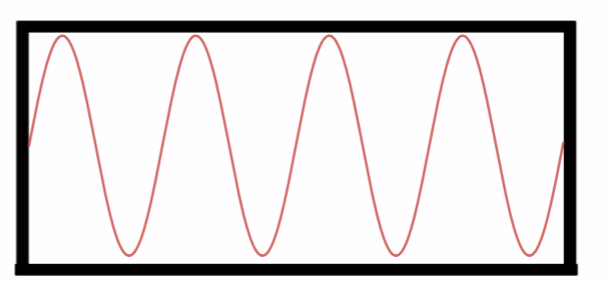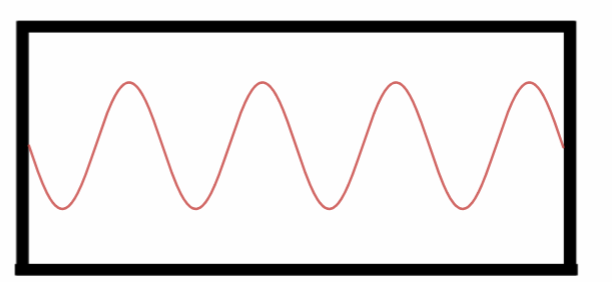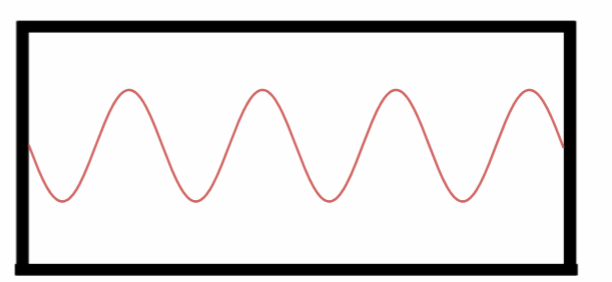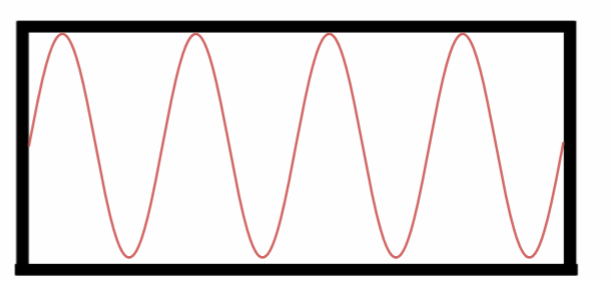
Sétimo Harmônico.

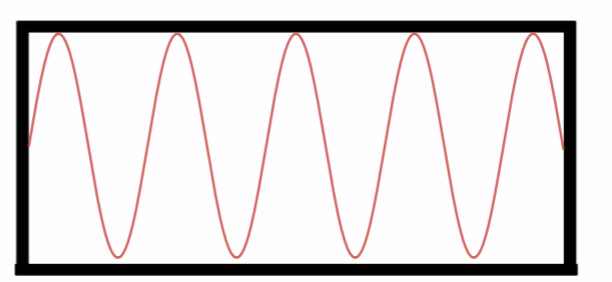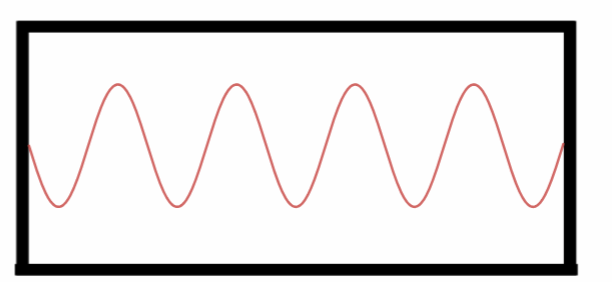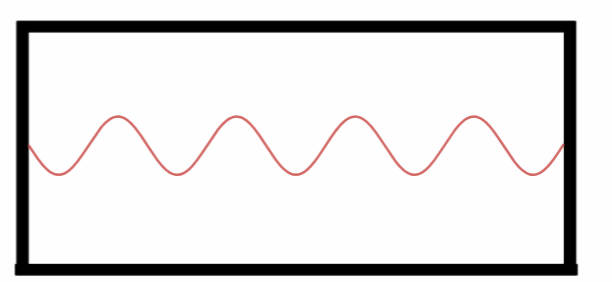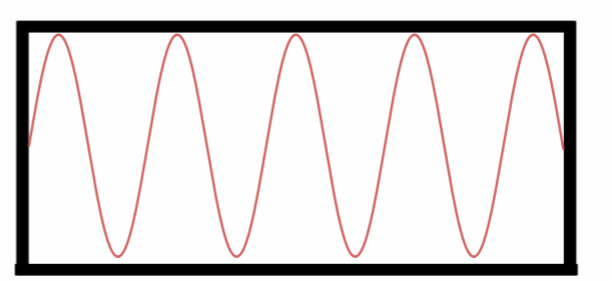
Oitavo Harmônico.

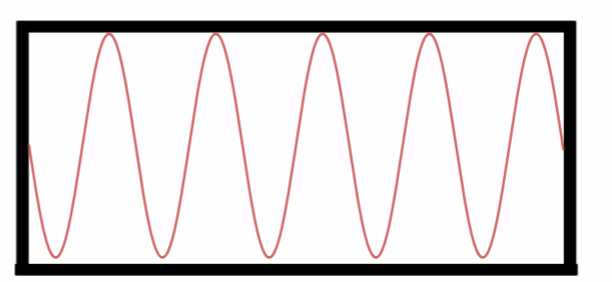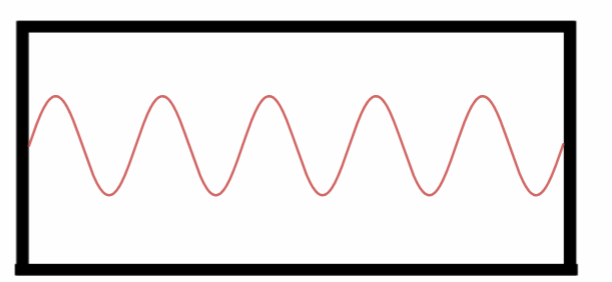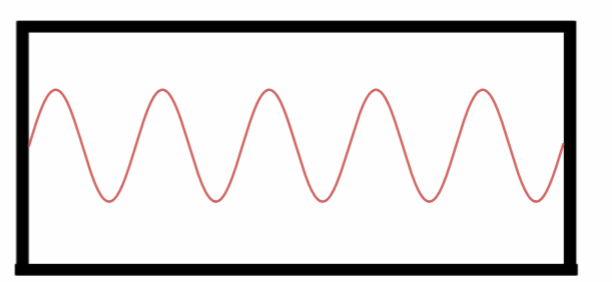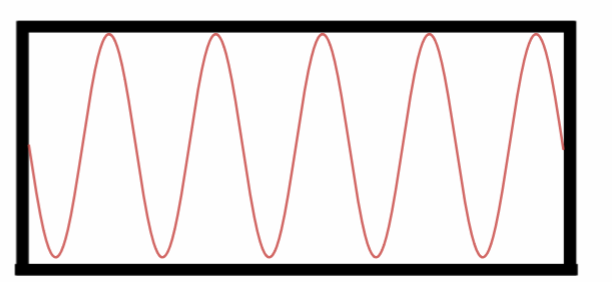
Nono Harmônico.

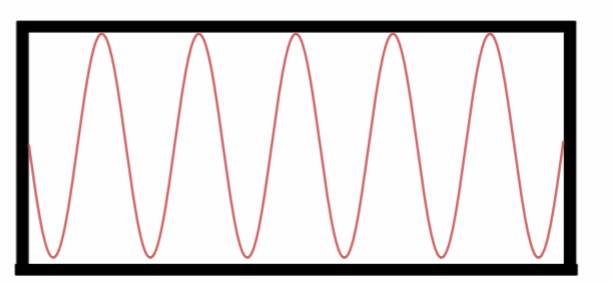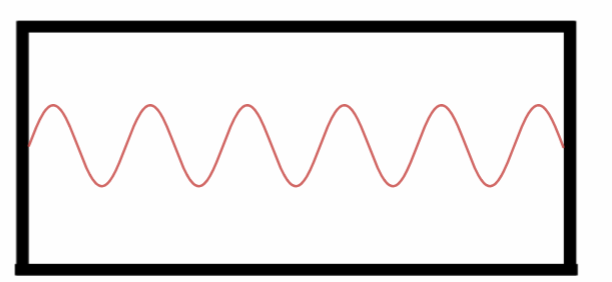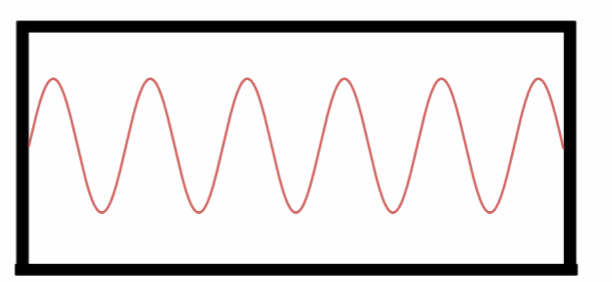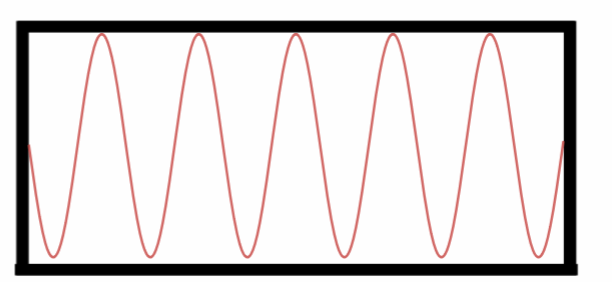
Décimo Harmônico.

Se estivermos falando de uma onda numa corda, podemos usar a equação de Taylor, isto é:

$$v=\sqrt{\frac{F}{\mu}}\Rightarrow$$

$$\lambda_n\cdot f_n=\sqrt{\frac{F}{\mu}}\Rightarrow$$

$$\frac{2L}{n}\cdot f_n=\sqrt{\frac{F}{\mu}}\Rightarrow$$

$$f_n=\frac{n}{2L} \sqrt{\frac{F}{\mu}}$$

Nos próximos casos, fica como exercício demonstrar tais relações, apresentadas a seguir. Alguns gifs estarão no corpo do texto para tentar auxiliar você a chegar nestas equações, mas os links no início do texto permite que você veja todos os harmônicos, basta clicar para exibir alguns gráficos.

Qualquer dúvida poste aí…

ONDA ESTACIONÁRIA COM AMBAS AS EXTREMIDADES LIVRES (OU TUBO COM AMBAS AS EXTREMIDADES ABERTAS – CHAMADO TUBO ABERTO)

Alguns harmônicos:

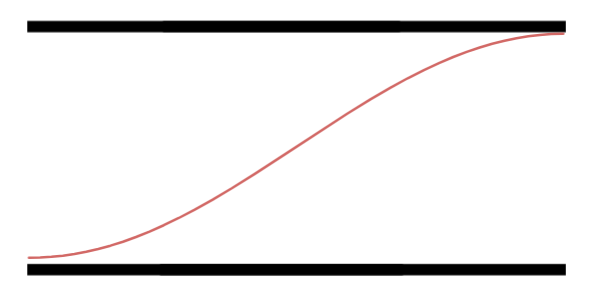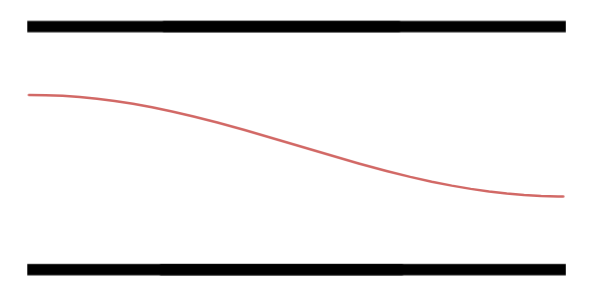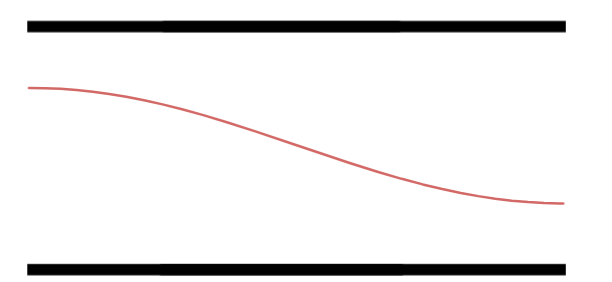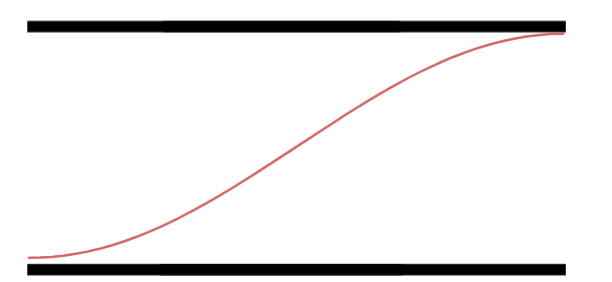
Primeiro Harmônico.

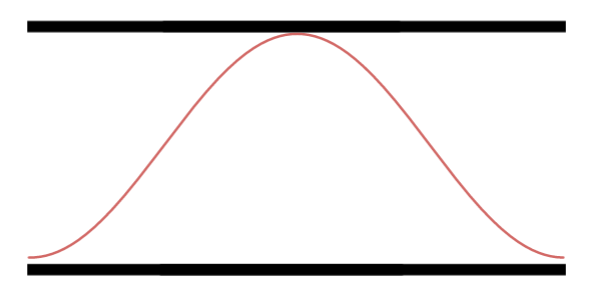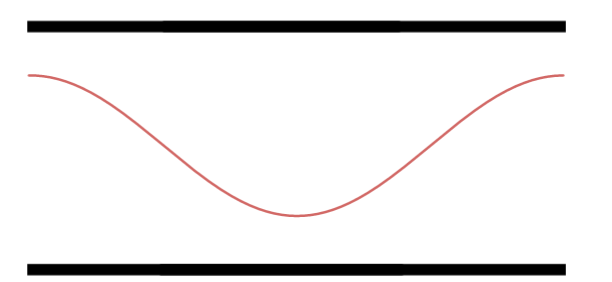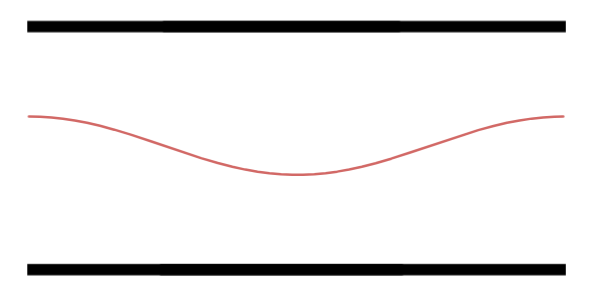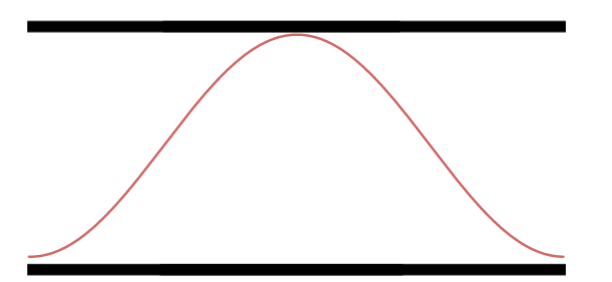
Segundo Harmônico.

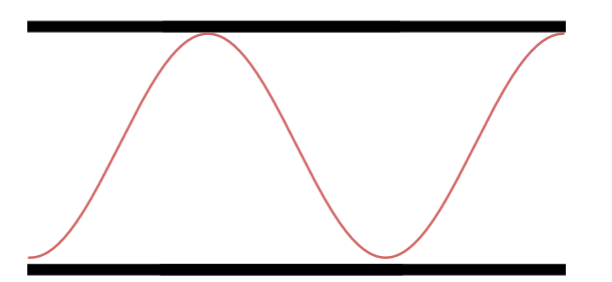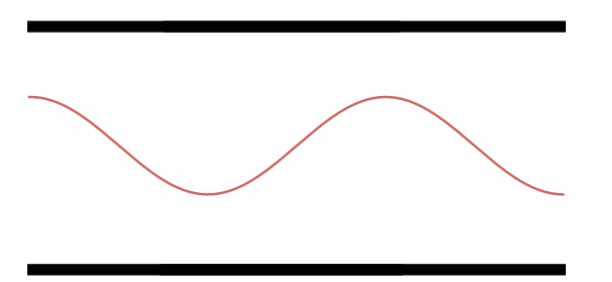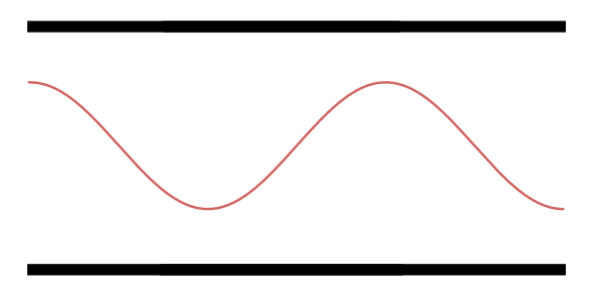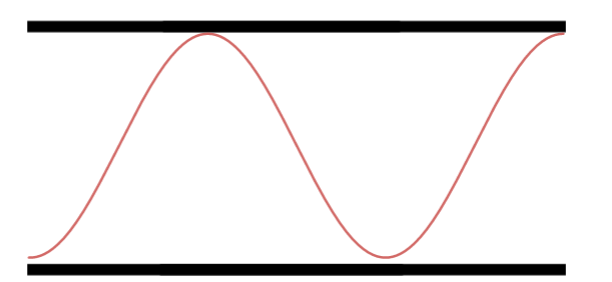
Terceiro Harmônico.

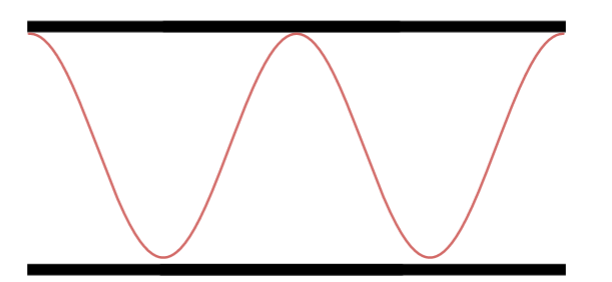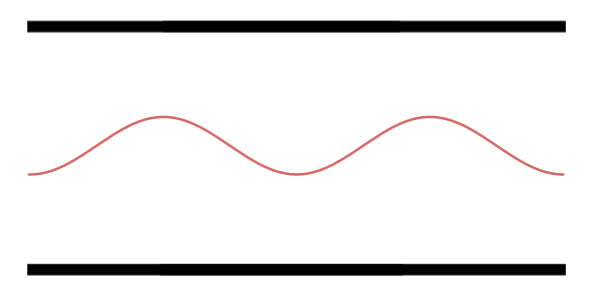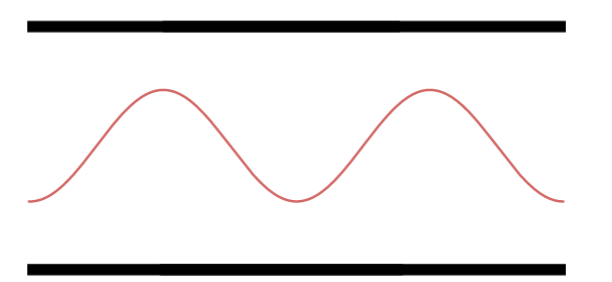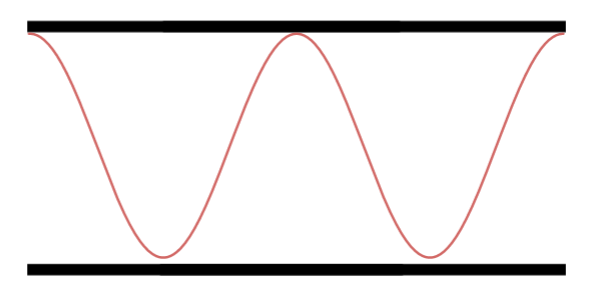
Quarto Harmônico.

Tente encontrar assim o seguinte padrão para o n-ésimo harmônico:

$$\lambda_n=\frac{2L}{n}$$

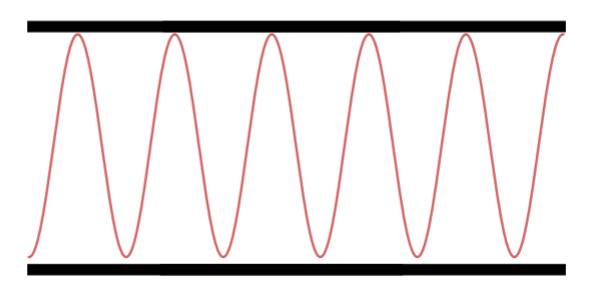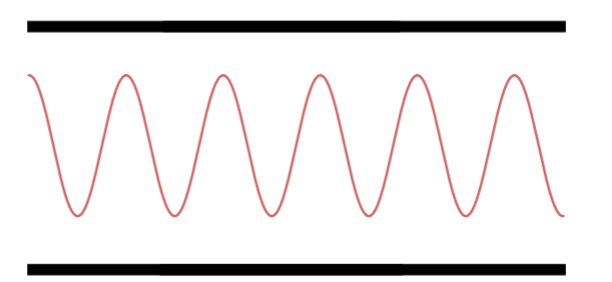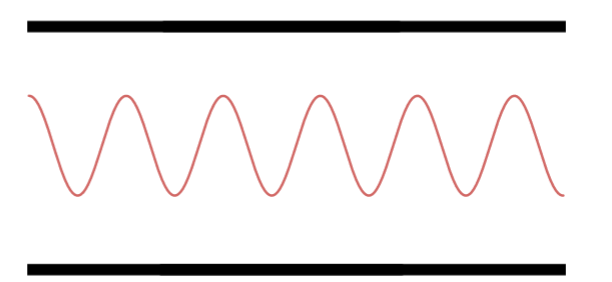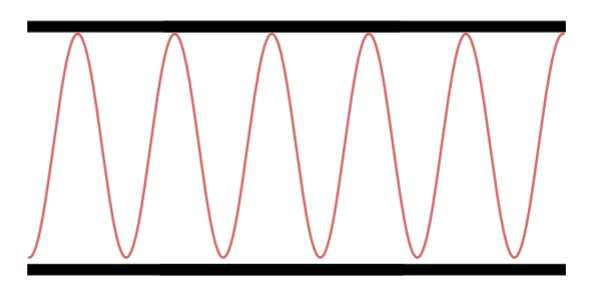
Décimo Harmônico.

O resultado é portanto igual ao anterior:

$$f_n=\frac{n}{2L} \sqrt{\frac{F}{\mu}}$$

ONDA ESTACIONÁRIA COM UMA DAS EXTREMIDADES LIVRE E OUTRA FIXA (OU TUBO COM UMA EXTREMIDADE ABERTA E OUTRA FECHADA – CHAMADO TUBO FECHADO)

Não fique esperando que neste último caso será igual… Na verdade, você verá (isso mesmo, tente desenhar num papel) que é possível colocar 1/4 de um comprimento de onda dentro do tubo, mas não 2/4, isto é, meio comprimento de onda. Você verá que somente um número ímpar de quarto de onda pode ser colocado dentro do tubo.

Faça os desenhos e tente verificar que

$$\lambda_n=\frac{4L}{n},\;\;n\;\;\text{ímpar}.$$

Veja as figuras e tente ver se verifica isto…

Primeiro Harmônico.

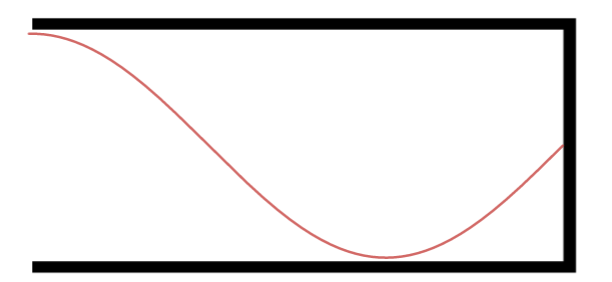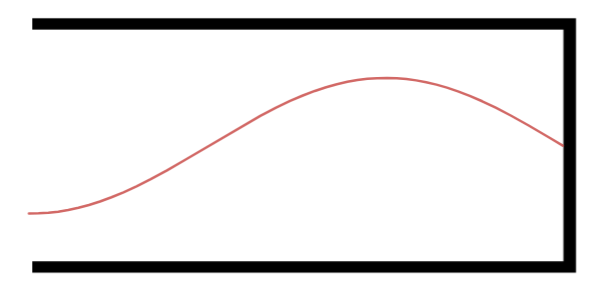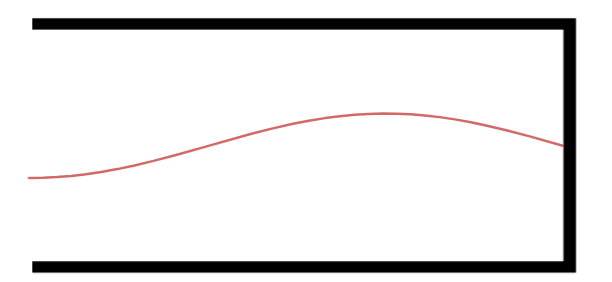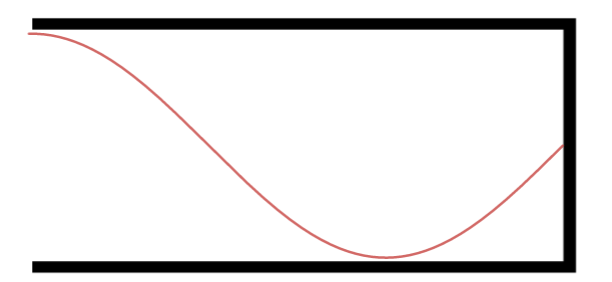
Terceiro Harmônico.

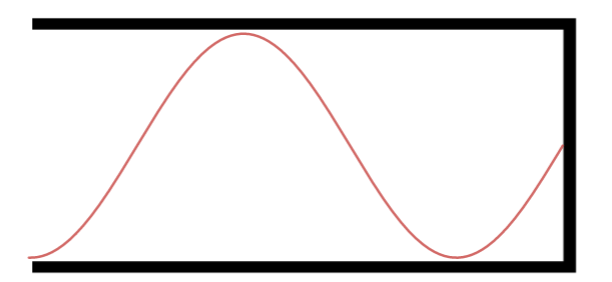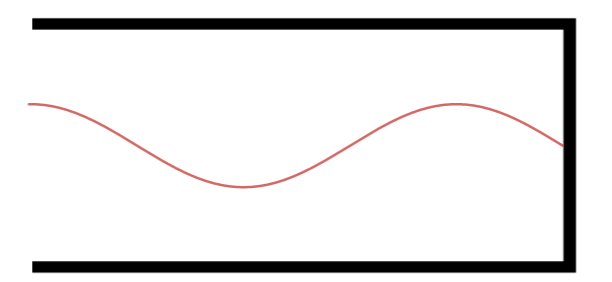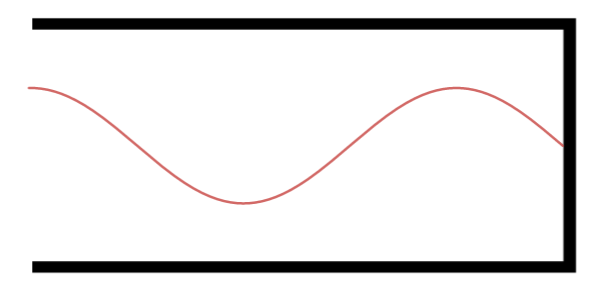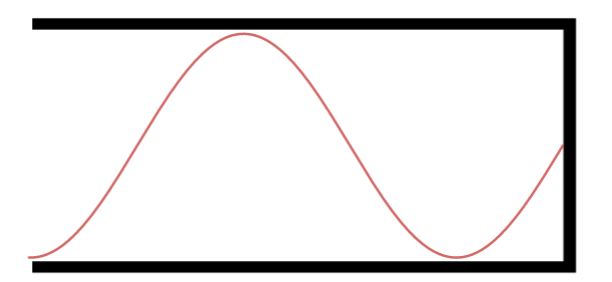
Quinto Harmônico.

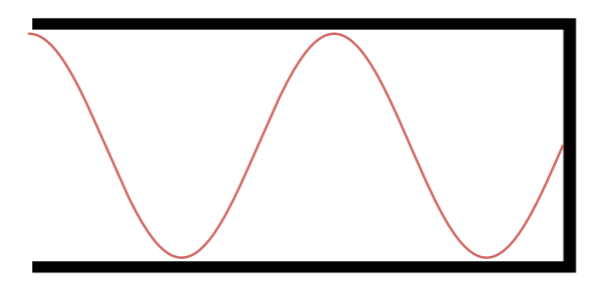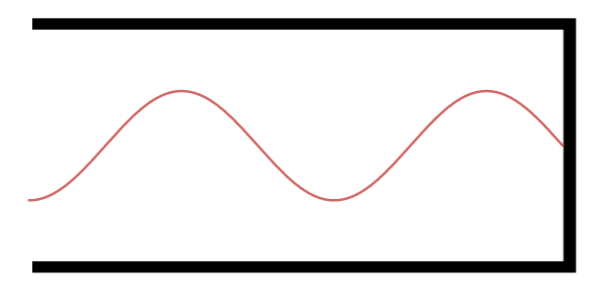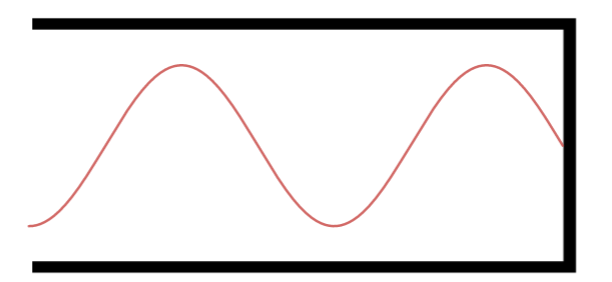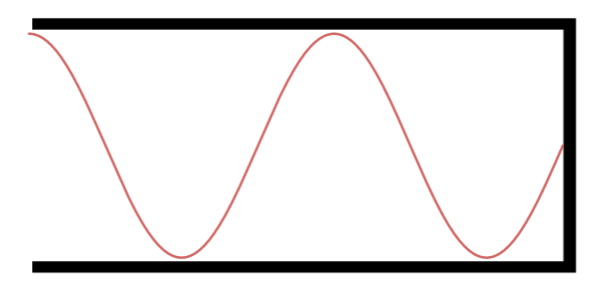
Sétimo Harmônico.

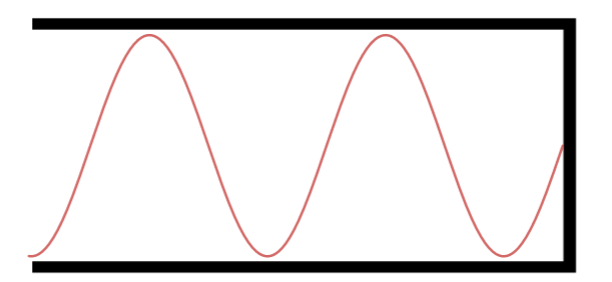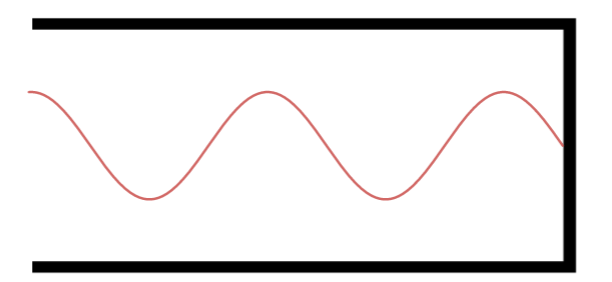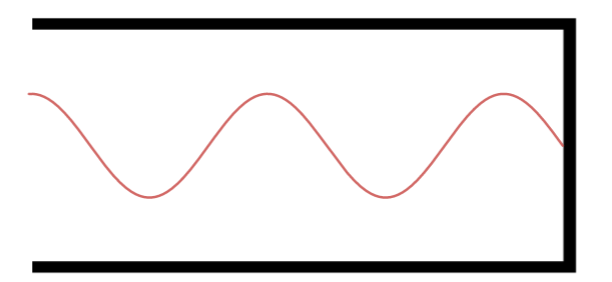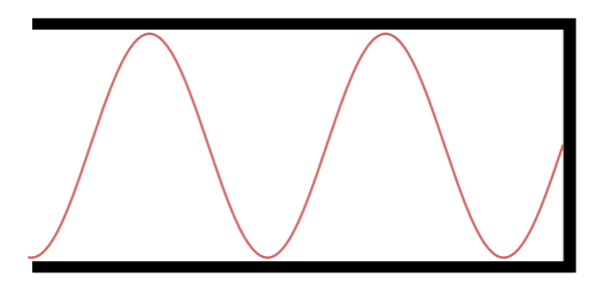
Nono Harmônico.

Observe e conte quantos quartos do comprimento de onda aparece em cada caso. Apenas para ilustrar, veja a configuração do 19° harmônico:

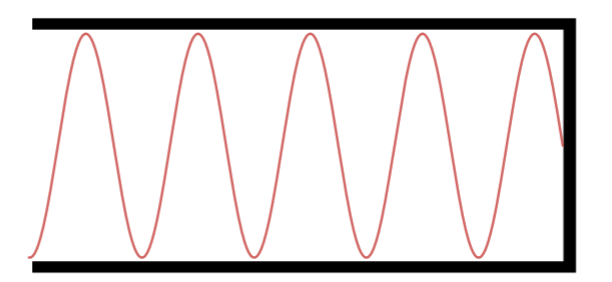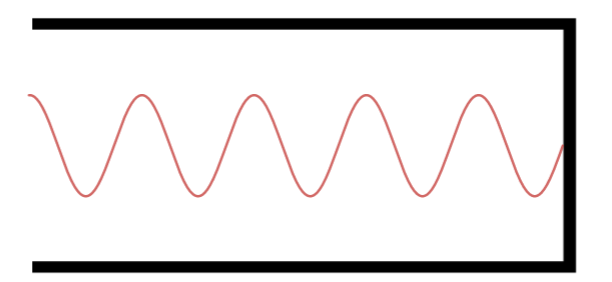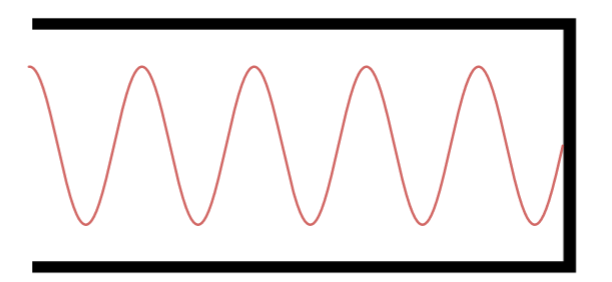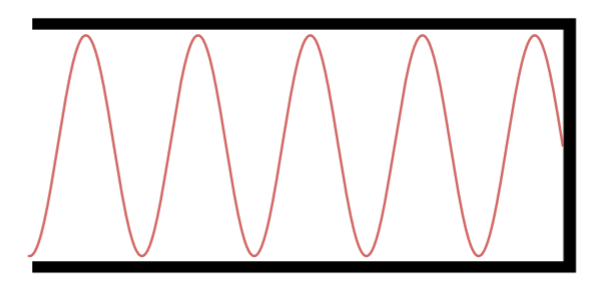
Décimo nono Harmônico.

Com isso tudo podemos verificar que

$$f_n=\frac{n}{4L} \sqrt{\frac{F}{\mu}},\;\;n\;\;\text{ímpar}$$

RESUMINDO

  • Cordas com duas extremidades fixas: $$f_n=\frac{n}{2L} \sqrt{\frac{F}{\mu}},\;\;n=1,\;2,\;3,\;4,\;5…$$
  • Cordas com ambas as extremidades livres: $$f_n=\frac{n}{2L} \sqrt{\frac{F}{\mu}},\;\;n=1,\;2,\;3,\;4,\;5…$$
  • Cordas com uma extremidade livre e outra fixa: $$f_n=\frac{n}{4L} \sqrt{\frac{F}{\mu}},\;\;n=1,\;3,\;5,\;7,\;9…$$

Sendo F a força de tração na corda pela qual a onda percorre e a densidade linear da corda dada por $$\mu=\frac m L$$ sendo m a massa da corda e L o comprimento da corda. Note que consideramos que o comprimento da corda é L e que mesmo com a onda na corda o comprimento da onda não se altera. Isso porque a amplitude das ondas são pequenas, portanto todas as figuras anteriores estão muito exageradas…

Exercícios sugeridos

Abaixo uma lista de exercício mais geral sobre ondulatória para você praticar.

http://fisica.professordanilo.com/download/2019/3COL/MC%203%20col%20Folha%2014%20Ondulat%C3%B3ria%20-%20Exerc%C3%ADcios%20Ondas%20Estacion%C3%A1rias.pdf

Bons estudos!

ENEM 2017 – Física

1 resposta

Em uma colisão frontal entre dois automóveis, a força que o cinto de segurança exerce sobre o tórax e abdômen do motorista pode causar lesões graves nos órgãos internos. Pensando na segurança do seu produto, um fabricante de automóveis realizou testes em cinco modelos diferentes de cinto. Os testes simularam uma colisão de 0,30 segundo de duração, e os bonecos que representavam os ocupantes foram equipados com acelerômetros. Esse equipamento registra o módulo da desaceleração do boneco em função do tempo. Os parâmetros como massa dos bonecos, dimensões dos cintos e velocidade imediatamente antes e após o impacto foram os mesmos para todos os testes. O resultado final obtido está no gráfico de aceleração por tempo.

Qual modelo de cinto oferece menor risco de lesão interna ao motorista?

a) 1

b) 2

c) 3

d) 4

e) 5

 

FUVEST 1ª FASE – 2012

1 resposta

Uma fibra óptica é um guia de luz, flexível e transparente, cilíndrico, feito de sílica ou polímero, de diâmetro não muito maior que o de um fio de cabelo, usado para transmitir sinais luminosos a grandes distâncias, c perdas de intensidade. A fibra óptica é constituída de um núcleo, por onde a luz se propaga e de um revestimento, como esquematizado na figura (corte longitudinal).
Sendo o índice de refração do núcleo 1,60 e o do revestimento, 1,45, o menor valor do ângulo de incidência θ do feixe luminoso, para que toda a luz incidente permaneça no núcleo, é, aproximadamente:

a) 45°

b) 50°

c) 55°

d) 60°

e) 65°

 

Interferência de ondas (pulsos)

4 respostas
Pulso em uma onda

Imagine que você tenha uma corda e nela você produz um pulso, como na figura a seguir.

Falha no carregamento

Um pulso se propagando em uma corda esticada.

No outro extremo da corda você produz novo pulso, de amplitude diferente. Digamos, com uma amplitude três vezes maior:

Pulso produzido em uma corda e se propagando para a esquerda.

Observe a figura a seguir se você não se lembra o que é amplitude de uma onda onde mostramos duas “fotografias” dos dois pulsos e comparamos as suas amplitudes.

As duas ondas são representadas na figura: note que um dos pulsos (o que se propaga para a esquerda) possui amplitude três vezes maior que a outra (que se propaga para a direita).

Interferência construtiva

Agora imagine que ambos os pulsos sejam produzidos simultaneamente: um se propagando para a direita, de amplitude A e outro para a esquerda de amplitude 3A, o que teríamos? Basta ver a figura a seguir:

Observe que quando as ondas ocupam o mesmo local na corda elas se sobrepõem. No final é como se somássemos duas funções matemáticas.

Para melhorar a visualização, veja a figura a seguir onde demos uma pausa no exato instante em que emas se sobrepõem e, na figura logo abaixo, mostramos uma “fotografia” desse instante. Ou seja, quando as ondas se sobrepõem, no exato instante da sobreposição elas se somam, mas logo após esse encontro (que chamamos de interferência) cada uma segue seu caminho como se nada tivesse acontecido.

Somando dois pulsos dando uma parada no exato momento de interferência construtiva (quando ambas as amplitudes apontam para um mesmo lado).

As figuras a seguir mostram instantâneos (“fotografias”) antes, durante e depois a interferência ou sobreposição.

Figura representando instantâneo da onda sendo representadas as velocidades dos pulsos e as amplitudes.

Instantâneo da sobreposição dos pulsos.

Instantâneo das ondas após a sobreposição.

Note portanto que a amplitude resultante é a soma das amplitudes:

$$A_{resultante}=A_1+A_2$$

Em nosso caso:

$$A_{resultante}=A+3A=4A$$

Observe que isto é válido em TODOS os instantes, não apenas no instante em que as ondas se sobrepõem.

Interferência destrutiva

Agora, imagine que dois pulsos sejam produzidos em oposição de fase, isto é, um possui crista para cima (digamos, o que se propaga para a direita com amplitude A) e o outro com crista para baixo (em oposição, portanto, o que se desloca para a esquerda, de amplitude -3A). Note que vamos considerar que para cima é positivo, assim, observando as figuras abaixo, que são auto-explicativas, vemos que as ondas se sobrepõem e, no caso das ondas serem da mesma forma, a amplitude resultante será a soma das amplitudes.

$$A_{resultante}=A+(-3A)=-2A$$

Pulsos com oposição de fase se interferindo.

Pulsos de ondas interferindo destrutivamente: três instantâneos mostrando antes, depois e no exato instante de máxima sobreposição.

Interferência totalmente destrutiva

Se as duas ondas que sofrem interferência destrutiva tiverem amplitudes de mesmo módulos, porém opostas (uma para cima e outra para baixo) em algum instante a interferência será totalmente destrutiva, ou seja, em um instante a onda deixa de ser visível e o fio fica retilíneo como se nenhuma onda existisse nele.

Veja as duas próximas animações onde apresentamos ondas interferindo-se em “tempo real” (próxima figura) e com uma pausa no exato instante de interferência destrutiva (figura posterior).

Duas ondas de amplitudes de sobrepondo.

Observe que cada quadro da animação foi sendo mostrado mais lentamente com o intuito de mostrar que, em certo instante, a sobreposição das ondas tona-se nula.

Simulação

Nada como tentar fazer você mesmo(a). A seguir disponibilizo as simulações para vocês brincarem um pouco.

 

E agora, esta preparado(a) para fazer alguns exercícios? No comentário deste artigo tem alguns links para exercícios externos, mas tem uma listinha daqui, do professordanilo.com

Clique aqui para baixar.

Equação de Taylor e a velocidade de uma onda em uma corda

Já que estamos falando de um pulso em uma corda, qual seria então a velocidade com que este pulso se propaga na corda?

A resposta é dada pela equação de Taylor apresentada a seguir:

$$v=\sqrt{\frac{F}{\mu}}$$

Sendo F a tração no fio, que no sistema internacional é medido em newtons (ou abreviadamente N). O outro termo, no denominador, é a densidade linear e se calcula dividindo a massa m do fio pelo seu comprimento L:

$$\mu=\frac m L$$

 





Lei de Coulomb e Campo Elétrico devido à uma carga elétrica puntiforme – Simulação

Deixe uma resposta

SIMULAÇÕES

Vamos direto aos links para as simulações, pois pode ser que seja por isso que você veio aqui.

SIMULAÇÃO DA LEI DE COULOMB.


SIMULAÇÃO DO CAMPO ELÉTRICO.

LEI DE COULOMB

Sejam duas cargas elétricas puntiformes \(Q\) e \(q\). Chamaremos esta segunda carga de carga de prova, pois se aproximamos a segunda carga da primeira é para determinar a força que a primeira faz na segunda.

Sabemos, da Lei de Coulomb, que a força entre estas duas cargas depende da distância \(d\) entre elas e da constante \(K\). Esta constante é chamada de constante eletrostática e se relaciona com a constante dielétrica \(k\), da permissividade elétrica do meio \(\varepsilon\) e permissividade elétrica do vácuo \(\varepsilon_0\):

$$K=\frac{1}{4\pi \varepsilon}$$ $$\varepsilon=k\cdot \varepsilon_0$$

É também ususal chamarmos a constante eletrostática no vácuo \(K_0\). Note também que o objetivo desta postagem é apresentar a simulação apenas, portanto sugiro que procure mais informações sobre Lie de Coulomb e sobre o experimento que possibilitou verificar que a Lei de Coulomb e determinar a constante eletrostática. Mesmo assim, vamos aqui apresentar a lei de Coulomb com base nas grandezas acima apresentadas.

Seja \(F\) o módulo da força \(\vec F\), a Lei de Coulomb nos afirma que:

$$F=\frac{K\cdot |Q|\cdot |q|}{d^2}.$$

Note que o que importa aqui que o que importa para determinar o módulo da força latex]\vec F[/latex] são os módulos das cargas \(Q\) e \(q\): \(|Q|\) e \(|q|\) respectivamente.

No link abaixo, você pode acessar a simulação para a Lei de Coulomb. Note como o módulo da força (tamanho da seta na simulação) varia sensivelmente com a distância entre as cargas.

SIMULAÇÃO DA LEI DE COULOMB.


CAMPO ELÉTRICO

Uma carga elétrica puntiforme de módulo \(|Q|\) produz um campo elétrico de módulo E a uma distância d da fonte (carga) dada por:

$$E=\frac{k|Q|}{d^2}.$$

No sistema internacional de Unidades, k é uma constante e proporcionalidade que vale

$$k=9\cdot 10^9 \rm \;N\cdot m^2/C^2.$$

Observe a simulação no link a seguir: nela, tocando ou clicando na tela, aparecerá uma seta cujo tamanho indica, de forma aproximadamente proporcional, o módulo do campo elétrico produzido por uma carga puntiforme (pequena, ou seja, do tamanho de um ponto). Para ter uma melhor noção espacial, com o uso do botão direito do mouse tocando e arrastando a tela, você pode ter uma visão de um outro ângulo do campo vetorial que você está criando. Tente você mesmo(a)!

SIMULAÇÃO DO CAMPO ELÉTRICO.